Цель работы: исследовать переходные процессы идеально-интегрирующего и апериодического первого порядка звеньев.
Общие положения
Анализ САУ удобно вести по эквивалентным структурным схемам, которые представляют собой соединение типовых динамических звеньев, имеющих определенную передаточную функцию. Передаточная функция представляет собой отношение изображений Лапласа выходного и входного сигналов элемента (системы) при нулевых начальных условиях. Зная правила преобразования структурных схем, определяют эквивалентную передаточную функцию системы и уравнение динамики системы. При исследовании динамических звеньев и системы используют регулярные сигналы:
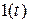 – единичное ступенчатое воздействие;
– единичное ступенчатое воздействие;
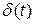 – единичный импульс;
– единичный импульс;
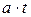 – линейно нарастающий сигнал;
– линейно нарастающий сигнал;
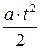 – сигнал с постоянным ускорением;
– сигнал с постоянным ускорением;
Как системы, так и звенья могут быть устойчивыми (статическими), нейтральными (астатическими) и неустойчивыми. Под устойчивостью понимают способность САУ или звена возвращаться в исходное состояние равновесия после приложения и снятия воздействия.
Под типовым динамическим звеном в ТАУ понимается часть САУ, описываемая в динамике алгебраическим или дифференциальным уравнением не выше 2-го порядка. Вид уравнения и определяет название звена. При подаче на вход типового звена регулярных сигналов можно определить его реакцию на данный вид сигнала.
Реакция на единичный ступенчатый сигнал 1(t) называется переходной характеристикой h(t); реакция на δ(t) – функция веса или импульсная переходная характеристика ω(t).
ω(t)=h'(t), т.к. δ(t)=1(t)'.
h(t) и ω(t) являются временными характеристиками звена.
При подаче на вход звена гармонического сигнала 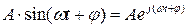 или
или 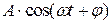 , на его выходе после завершения переходного процесса также наблюдаются колебания.
, на его выходе после завершения переходного процесса также наблюдаются колебания.
Частотные свойства звена определяются комплексным коэффициентом передачи:
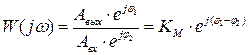 , (1)
, (1)
который представляет собой отношение комплексных амплитуд сигналов на выходе и на входе при подаче на вход гармонического сигнала. При изменении частоты входного сигнала от 0 до ∞ можно исследовать спектр входного и выходного сигналов, т.е. получить АФЧХ – амплитудно-фазовую частотную характеристику – траекторию движения конца вектора комплексного коэффициента передачи W(jω), при изменении частоты от 0 до ∞. АФЧХ отражает соотношение амплитуд и фаз сигналов на выходе и входе.
При нулевых начальных условиях уравнение звена в изображениях записывается в виде:
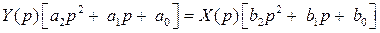 , (2)
, (2)
где Y(p), X(p) – изображение по Лапласу выходной и входной величин;
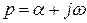 – комплексная переменная (оператор Лапласа).
– комплексная переменная (оператор Лапласа).
Запишем передаточную функцию, соответствующую уравнению (2):
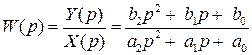 , (3)
, (3)
где 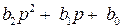 – входной полином;
– входной полином;
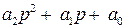 – выходной полином.
– выходной полином.
Обычно принято все члены уравнения динамики (2) делить на свободный член – коэффициент 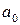 , тогда уравнение записывают таким образом:
, тогда уравнение записывают таким образом:
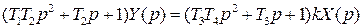 , (4)
, (4)
где 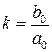 – коэффициент усиления, размерность которого зависит от Y и X;
– коэффициент усиления, размерность которого зависит от Y и X;
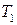 ,
, 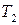 ,
, 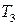 ,
, 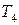 – постоянные коэффициенты, обычно имеющие размерность времени;
– постоянные коэффициенты, обычно имеющие размерность времени;
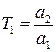 ,
, 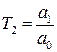 ,
, 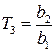 ,
, 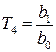 .
.
Линейные динамические звенья принято классифицировать по виду уравнения динамики: на простейшие (безинерционное, идеально-дифференцирующее, идеально-интегрирующее), звенья 1-го и звенья 2-го порядка.
Реакция звена на входной сигнал произвольной формы может быть определена по известной передаточной функции его через обратное преобразование Лапласа:
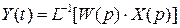
или решая дифференциальное уравнение при известных начальных условиях и входном сигнале. Если входной сигнал 1(t), т.е.
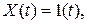
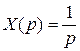 .
.
то определяется переходная функция типовых звеньев h(t):
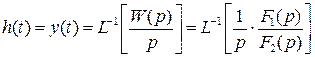
где 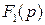 ,
, 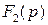 – полиномы входной и выходной.
– полиномы входной и выходной.
Она находится по таблицам, либо по теореме разложения Хэвисайда:
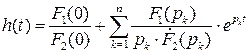 , (5)
, (5)
где 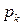 – k-тый корень полинома знаменателя
– k-тый корень полинома знаменателя 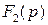 ;
;
n – число корней (степень полинома 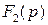 );
);
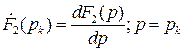 .
.
Изображение по Лапласу гармонических сигналов:
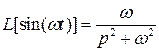 ;
;
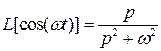 .
.
Таким образом, через обратное преобразование Лапласа может быть определена реакция на любой входной сигнал.
Звенья 1-го и 2-го порядков можно сформировать на основе блока «интегратор» (идеально-интегрирующего звена), вводя обратные связи.
Поэтому при исследовании переходных процессов типовых звеньев необходимо хорошо представлять реакцию идеально-интегрирующего звена на различные типы воздействий.
Уравнение динамики интегрирующего звена выглядит следующим образом:
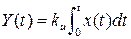 или
или 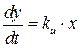 ,
, 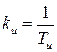 .
.
Передаточная функция интегрирующего звена и комплексный коэффициент передачи записываются:
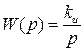 и
и 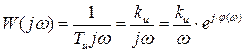 ,
, 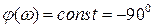 .
.
В соответствии с уравнением (5) переходная характеристика – прямая линия с угловым коэффициентом, зависящим от 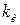 (рисунок 2.1).
(рисунок 2.1).
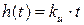 ,
, 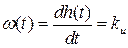 ,
, 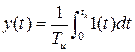 .
.
Скорость изменения выходной величины такого звена пропорциональна входной величине.
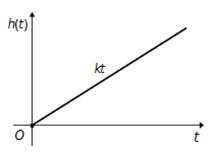
Рисунок 2.1 – Переходная характеристика идеально интегрирующего звена
Передаточная функция апериодического звена:
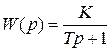 .
.
Уравнение переходной характеристики: 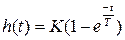 .
.
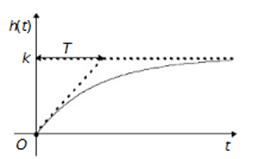
Рисунок 2.2 – Переходная характеристика апериодического звена 1-го порядка
Порядок выполнения лабораторной работы
 2015-02-04
2015-02-04 2750
2750

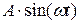 –
–