Исследование переходных процессов типовых динамических звеньев первого порядка (реально-дифференцирующего и инерционно-форсирующего)

Цель работы: исследовать переходные процессы идеально-интегрирующего и апериодического первого порядка звеньев.

Общие положения

Реально-дифференцирующее (дифференцирующее с замедлением) звено получается при последовательном соединении идеально-дифференцирующего и апериодического 1-го порядка звеньев или введением интегрирующего звена в обратную связь к усилителю (рисунок 3.3).

Дифференциальное уравнение такого звена:

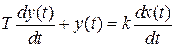
и ему соответствует передаточная функция и комплексный коэффициент передачи вида:

; .

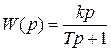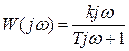Фазочастотная характеристика этого звена получается суммированием ФЧХ составляющих звеньев.

.

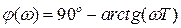Переходная характеристика реально-дифференцирующего звена совпадает с импульсной переходной характеристикой апериодического звена 1-го порядка (рисунок 3.1).

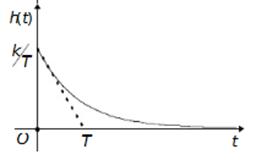
Рисунок 3.1 – Переходная характеристика реально дифференцирующего звена

Инерционно-форсирующее звено можно рассматривать как последовательное соединение инерционного 1-го порядка и форсирующего звеньев, может быть получено введением инерционной обратной связи к усилителю (рисунок 3.4).

Это звено описывается следующим дифференциальным уравнением:

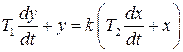
и его передаточная функция, и комплексный коэффициент усиления, соответственно:

; .

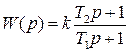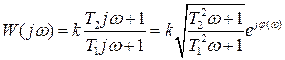и фазочастотная характеристика:

.

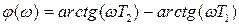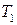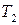Свойства инерционно-форсирующего звена и все временные и частотные характеристики зависят от соотношения величин и , где 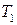– постоянная времени инерционного звена, 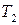– постоянная времени форсирующего звена.

Если 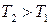, то звено ближе по своим свойствам к форсирующему звену (рисунок 3.2, б). Если 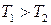, то звено по своим свойствам ближе к апериодическому (рисунок 3.2, а).

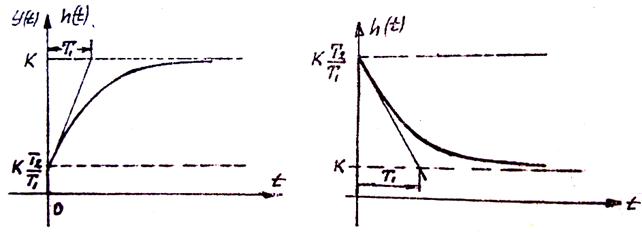
Рисунок 3.2 – Переходная характеристика инерционно-форсирующего звена

Порядок выполнения лабораторной работы