2015-02-04
4360
Цель работы: исследовать переходные процессы в звеньях второго порядка (апериодическом, колебательном и консервативном).
Общие положения
Звенья 2-го порядка описываются в динамике дифференциальными уравнениями 2-го порядка.
.
.
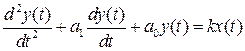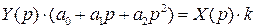Характеристическое уравнение звена второго порядка:
.
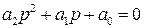В зависимости от соотношения коэффициентов характеристического уравнения, корни могут быть действительными, такое звено называется апериодическим звеном 2-го порядка; если корни комплексные, то звено называется колебательным; при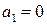 
звено называется консервативным.
Рассмотрим колебательное звено, описываемое следующим дифференциальным уравнением:
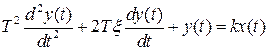
и, соответственно, имеющим передаточную функцию:
,
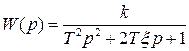где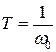 
– постоянная времени;
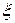– коэффициент демпфирования, степень затухания;
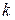– передаточный коэффициент.
Запишем характеристическое уравнение:
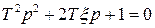или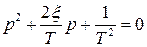 
.
тогда корни его:
,
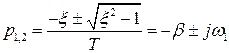где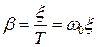 
– коэффициент затухания колебаний.
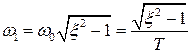– собственная частота колебаний звена.
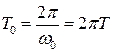– период резонансных колебаний.
Если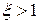 
, то корни уравнения вещественные отрицательные и переходный процесс будет монотонным (рисунок 4.1 (1)) и определяется выражением:
,
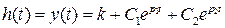где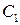 
и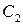 
– постоянные интегрирования, определяемые по начальным условиям. Т.е. звено является апериодическим 2-го порядка.
При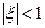 
– корни комплексные и, если 
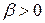, то переходный процесс представляет собой затухающие колебания (рисунок 4.2). Именно такое звено называется устойчивым колебательным.
Уравнение переходной характеристики имеет вид:
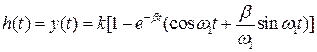
При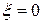 
– получаем мнимые корни 
.
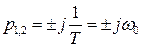Переходный процесс такого звена – незатухающие колебания с частотой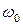 
и звено называю консервативным (рисунок 4.4).
Если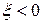 
, то вещественная часть корней характеристического уравнения становится положительной, а значит, звено будет неустойчиво, а вид переходного процесса опять будет определяться выражением 
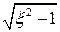. При действительных корнях – переходный процесс также будет представлять сумму экспонент, уходящих в ∞ при 
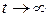(рисунок 4.1 (2)).
При комплексных корнях с положительной вещественной частью получим расходящиеся колебания – неустойчивое колебательное звено (рисунок 4.3).
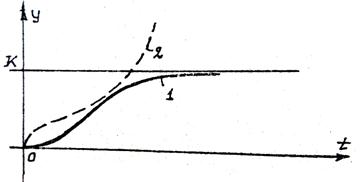
Рисунок 4.1 – Монотонный переходный процесс (1 – устойчивый; 2 – неустойчивый)
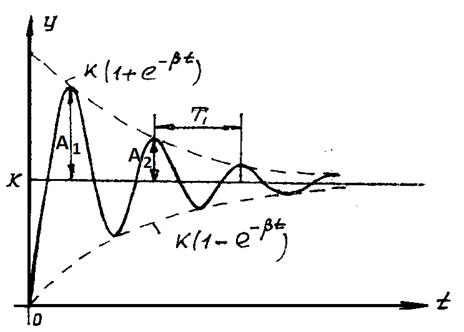
Рисунок 4.2 – Колебательный затухающий переходный процесс
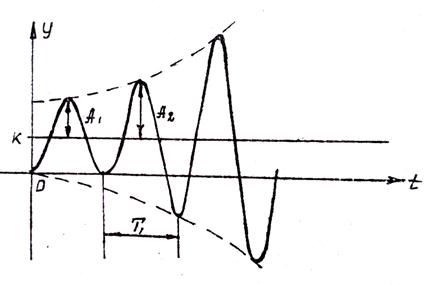
Рисунок 4.3 – Колебательный расходящийся переходный процесс
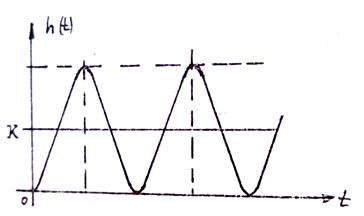
Рисунок 4.4 – Колебательный незатухающий переходный процесс
Вид переходной характеристики h(t) зависит от коэффициента ξ. Следует помнить, что колебания возникают лишь в том случае, если корни характеристического уравнения являются комплексными величинами, т.е. ес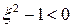ли 
или .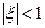
Для устойчивого колебательного звена 0<ξ<1 и амплитуда колебаний затухает по экспоненте – по уравнению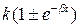 
.
Для неустойчивого колебательного звена ξ<0, амплитуда колебаний с течением времени возрастает по уравнению .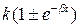
Если корни характеристического уравнения действительные отрицательные, то звено является апериодическим 2-го порядка (т.е. при ξ>1) и может быть представлено в виде последовательного соединения двух апериодических звеньев с постоянными времен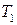и 
и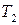 
.
Оно описывается дифференциальным уравнением:
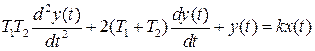
и передаточной функцией:
.
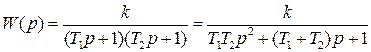Порядок выполнения лабораторной работы
