Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты 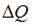 . На совершение газом работы расходуется часть теплоты
. На совершение газом работы расходуется часть теплоты 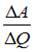 , равная …
, равная …
 | 0,4 | ||
| 0,6 | |||
| 0,7 | |||
| 0,3 |
Решение:
Изменение внутренней энергии газа равно 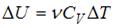 . Количество теплоты, переданное газу при изобарическом процессе, можно определить по формуле
. Количество теплоты, переданное газу при изобарическом процессе, можно определить по формуле 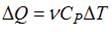 . Согласно I началу термодинамики,
. Согласно I началу термодинамики, 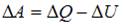 . Тогда
. Тогда 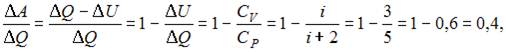 где
где 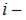 число степеней свободы молекулы, для одноатомного газа
число степеней свободы молекулы, для одноатомного газа 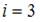 .
.
Тема: Первое начало термодинамики. Работа при изопроцессах
Одному молю двухатомного газа было передано 5155 Дж теплоты, при этом газ совершил работу, равную 1000 Дж, а его температура повысилась на ______ K.
| 200 | |
Решение:
Согласно первому началу термодинамики 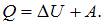 Изменение внутренней энергии
Изменение внутренней энергии 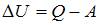 , с другой стороны –
, с другой стороны – 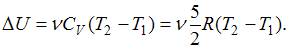
Следовательно, 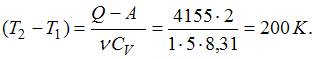
Тема: Первое начало термодинамики. Работа при изопроцессах
При адиабатическом расширении 2 молей одноатомного газа его температура понизилась с 300 К до 200 К, при этом газ совершил работу (в Дж), равную …
|
|
|
| 2493 | |
Решение:
При адиабатическом расширении работа газа находится по формуле: 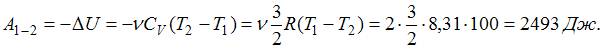
Тема: Первое начало термодинамики. Работа при изопроцессах
При адиабатическом расширении 2 молями одноатомного газа совершена работа, равная 2493 Дж. При этом изменение температуры составило _____ K.
Тема: Первое начало термодинамики. Работа при изопроцессах
Один моль идеального одноатомного газа в ходе некоторого процесса получил 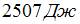 теплоты. При этом его температура понизилась на
теплоты. При этом его температура понизилась на 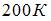 . Работа (
. Работа (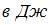 ), совершенная газом, равна …
), совершенная газом, равна … 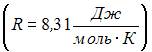
| 5000 | |
Решение:
Согласно первому началу термодинамики, 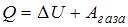 , где
, где 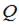 – количество теплоты, полученное газом,
– количество теплоты, полученное газом, 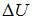 – приращение его внутренней энергии,
– приращение его внутренней энергии, 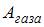 – работа, совершенная газом. Отсюда
– работа, совершенная газом. Отсюда 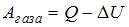 . Приращение внутренней энергии в данном случае
. Приращение внутренней энергии в данном случае 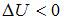 , так как температура газа в ходе процесса понизилась.
, так как температура газа в ходе процесса понизилась. 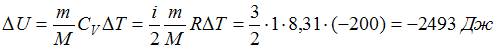 . Тогда работа, совершенная газом, равна
. Тогда работа, совершенная газом, равна 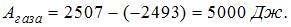
Тема: Первое начало термодинамики. Работа при изопроцессах
Идеальному одноатомному газу в изобарном процессе подведено количество теплоты 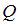 . При этом на увеличение внутренней энергии газа расходуется ________% подводимого количества теплоты.
. При этом на увеличение внутренней энергии газа расходуется ________% подводимого количества теплоты.
| 60 | |
Решение:
Согласно первому началу термодинамики, 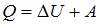 , где
, где 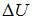 – приращение внутренней энергии,
– приращение внутренней энергии, 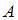 – работа газа. Изменение внутренней энергии
– работа газа. Изменение внутренней энергии 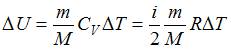 . Работа газа при изобарном процессе
. Работа газа при изобарном процессе 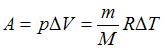 . Тогда
. Тогда 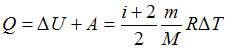 . Доля количества теплоты, расходуемого на увеличение внутренней энергии, составит
. Доля количества теплоты, расходуемого на увеличение внутренней энергии, составит 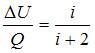 . Для одноатомного газа
. Для одноатомного газа 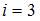 . Следовательно,
. Следовательно, 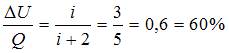 .
.
Тема: Первое начало термодинамики. Работа при изопроцессах
При адиабатическом расширении 2 молями одноатомного газа совершена работа, равная 2493 Дж. При этом изменение температуры составило _____ K.
|
|
|
| 100 | |
Решение:
При адиабатическом расширении работа газа находится по формуле: 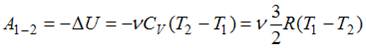 ; следовательно,
; следовательно, 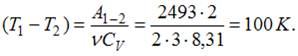
Тема: Первое начало термодинамики. Работа при изопроцессах
Идеальному газу сообщается одинаковое количество теплоты при изохорном (1), изобарном (2) и изотермическом (3) процессах. Для совершаемых газом работ справедливы соотношения …
 | 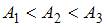 | ||
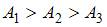 | |||
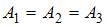 | |||
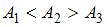 |
Решение:
Согласно I началу термодинамики для различных изопроцессов имеем: 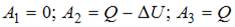 . Следовательно,
. Следовательно, 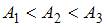 .
.
Тема: Первое начало термодинамики. Работа при изопроцессах
Идеальному трехатомному газу (с нелинейными молекулами) в изобарном процессе подведено количество теплоты 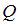 . При этом на работу расширения расходуется ________% подводимого количества теплоты. (Считать связь атомов в молекуле жесткой.)
. При этом на работу расширения расходуется ________% подводимого количества теплоты. (Считать связь атомов в молекуле жесткой.)
| 25 | |
Решение:
Согласно первому началу термодинамики, 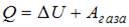 , где
, где 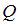 – количество теплоты, полученное газом,
– количество теплоты, полученное газом, 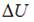 – приращение его внутренней энергии,
– приращение его внутренней энергии, 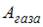 – работа, совершенная газом. Изменение внутренней энергии
– работа, совершенная газом. Изменение внутренней энергии 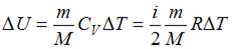 . Работа газа при изобарном процессе
. Работа газа при изобарном процессе 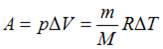 . Тогда
. Тогда 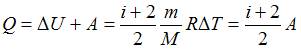 . Доля количества теплоты, расходуемого на работу расширения, составит
. Доля количества теплоты, расходуемого на работу расширения, составит 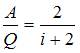 . Для трехатомного газа с жесткой связью атомов в молекуле
. Для трехатомного газа с жесткой связью атомов в молекуле 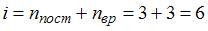 . Следовательно,
. Следовательно, 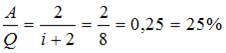 .
.
Тема: Первое начало термодинамики. Работа при изопроцессах
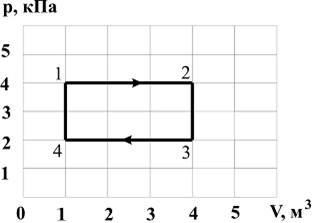
Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы при нагревании к работе газа за весь цикл по модулю равно …
| 2 | |
Решение:
Работа газа за цикл в координатных осях 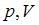 численно равна площади фигуры, ограниченной диаграммой кругового процесса.
численно равна площади фигуры, ограниченной диаграммой кругового процесса. 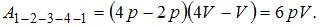 Работа при нагревании газа численно равна площади под графиком процесса 1 – 2:
Работа при нагревании газа численно равна площади под графиком процесса 1 – 2: 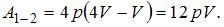 Отношение работ, совершенных в этих процессах, равно:
Отношение работ, совершенных в этих процессах, равно: 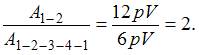 Модуль отношения:
Модуль отношения: 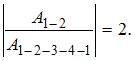
Тема: Первое начало термодинамики. Работа при изопроцессах
На рисунке представлена диаграмма циклического процесса идеального одноатомного газа:
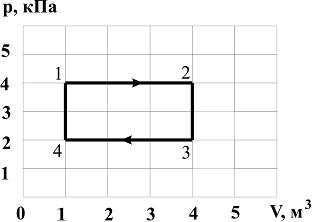
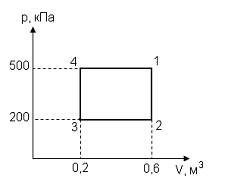
За цикл газ получает количество теплоты (в 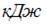 ), равное …
), равное …
| 33 | |
Решение:
Цикл состоит из изохорного нагревания (4–1), изобарного расширения (1–2), изохорного охлаждения (2–3) и изобарного сжатия (3–4). На первых двух этапах цикла газ получает теплоту. Согласно первому началу термодинамики, количество теплоты, получаемое газом, равно 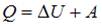 , где
, где 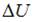 – изменение внутренней энергии,
– изменение внутренней энергии, 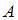 – работа газа. Тогда
– работа газа. Тогда 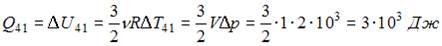 .
.
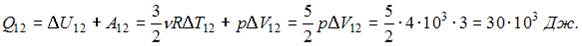
Таким образом, количество теплоты, получаемое газом за цикл, равно 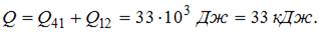
Тема: Первое начало термодинамики. Работа при изопроцессах
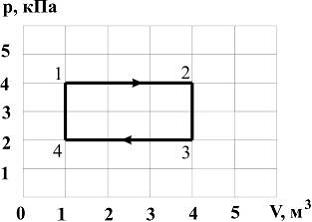
В процессе, представленном на рисунке, работа идеального одноатомного газа (в кДж) при нагревании равна …
 | |||
Решение:
Работа газа в координатных осях 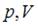 численно равна площади под графиком функции. Работа при нагревании совершается в процессе
численно равна площади под графиком функции. Работа при нагревании совершается в процессе 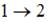 .
. 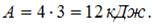
Тема: Первое начало термодинамики. Работа при изопроцессах
Работа идеального одноатомного газа (в кДж) в циклическом процессе, представленном на рисунке, равна …
 | |||
Тема: Первое начало термодинамики. Работа при изопроцессах
При изотермическом расширении 1 моля газа его объем увеличился в 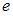 раз (
раз (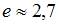 ), работа газа составила 1662 Дж. Тогда температура равна _____ K.
), работа газа составила 1662 Дж. Тогда температура равна _____ K.
| 200 | |
Решение:
При изотермическом расширении работа газа находится по формуле: 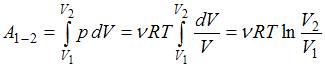 ; следовательно, температура газа равна:
; следовательно, температура газа равна: 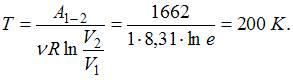
Тема: Первое начало термодинамики. Работа при изопроцессах
Одному молю двухатомного газа было передано 5155 Дж теплоты, при этом газ совершил работу, равную 1000 Дж, а его температура повысилась на ______ K.
Тема: Второе начало термодинамики. Энтропия
При поступлении в неизолированную термодинамическую систему тепла в ходе обратимого процесса для приращения энтропии верным будет соотношение …
|
|
|
 | 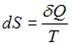 | ||
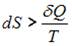 | |||
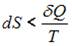 | |||
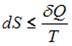 |
Решение:
Отношение 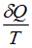 в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией
в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией 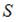 системы:
системы: 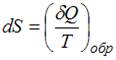 . В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах:
. В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах: 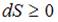 . Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса:
. Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса: 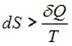 .
.
Тема: Второе начало термодинамики. Энтропия
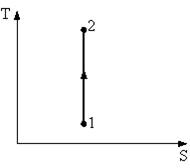
Процесс, изображенный на рисунке в координатах (T, S), где S – энтропия, является …
 | адиабатным сжатием | ||
| изохорным нагреванием | |||
| изобарным расширением | |||
| изотермическим расширением |
Решение:
Адиабатные процессы происходят без теплообмена с окружающей средой, то есть система не получает тепла и не отдает его, 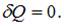 Изменение энтропии определяется как
Изменение энтропии определяется как 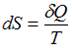 , следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном сжатии над газом совершают работу внешние силы, внутренняя энергия увеличивается:
, следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном сжатии над газом совершают работу внешние силы, внутренняя энергия увеличивается: 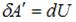 , температура газа увеличивается. Следовательно, процесс
, температура газа увеличивается. Следовательно, процесс 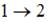 является адиабатическим сжатием.
является адиабатическим сжатием.
Тема: Второе начало термодинамики. Энтропия
Процесс, изображенный на рисунке в координатах (T, S), где S – энтропия, является …
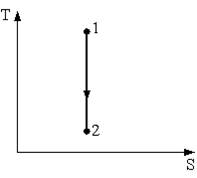
 | адиабатным расширением | ||
| изохорным охлаждением | |||
| изобарным сжатием | |||
| изотермическим сжатием |
Решение:
Адиабатные процессы происходят без теплообмена с окружающей средой, то есть система не получает тепла и не отдает его, 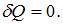 Изменение энтропии определяется как
Изменение энтропии определяется как 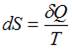 , следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном расширении газ совершает работу над внешними силами, внутренняя энергия уменьшается:
, следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном расширении газ совершает работу над внешними силами, внутренняя энергия уменьшается: 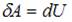 , температура газа уменьшается. Следовательно, процесс
, температура газа уменьшается. Следовательно, процесс 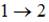 является адиабатным расширением.
является адиабатным расширением.
Тема: Второе начало термодинамики. Энтропия
При адиабатическом сжатии идеального газа …
|
|
|
 | температура возрастает, энтропия не изменяется | ||
| температура возрастает, энтропия убывает | |||
| температура и энтропия возрастают | |||
| температура не изменяется, энтропия возрастает |
Решение:
Адиабатные процессы происходят без теплообмена с окружающей средой, то есть система не получает тепла и не отдает его, 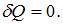 Изменение энтропии определяется как
Изменение энтропии определяется как 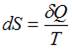 , следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном сжатии над газом совершают работу внешние силы, внутренняя энергия увеличивается:
, следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном сжатии над газом совершают работу внешние силы, внутренняя энергия увеличивается: 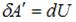 , температура газа увеличивается.
, температура газа увеличивается.
Тема: Второе начало термодинамики. Энтропия
В идеальной тепловой машине из каждого 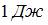 теплоты, получаемого от нагревателя,
теплоты, получаемого от нагревателя, 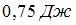 отдается холодильнику. Если температура холодильника 27°С, то температура нагревателя (в °С) равна …
отдается холодильнику. Если температура холодильника 27°С, то температура нагревателя (в °С) равна …
 | |||
Решение:
Коэффициент полезного действия тепловой машины определяется соотношением 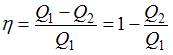 , где
, где 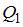 и
и 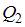 – количество теплоты, полученное от нагревателя и отданное холодильнику соответственно. Для идеальной тепловой машины
– количество теплоты, полученное от нагревателя и отданное холодильнику соответственно. Для идеальной тепловой машины 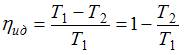 (
(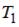 и
и 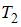 – температура нагревателя и холодильника соответственно). Приравнивая правые части этих выражений, получаем
– температура нагревателя и холодильника соответственно). Приравнивая правые части этих выражений, получаем 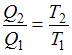 . Отсюда
. Отсюда 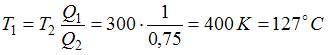 .
.
 2015-02-04
2015-02-04 10395
10395
