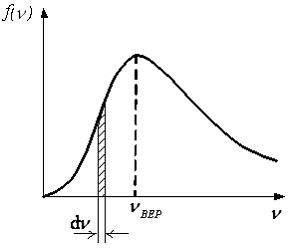
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 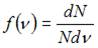 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 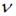 до
до 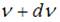 в расчете на единицу этого интервала.
в расчете на единицу этого интервала.
Для этой функции верным является утверждение, что с увеличением температуры:
 | максимум кривой смещается вправо | ||
| площадь под кривой увеличивается | |||
| величина максимума функции увеличивается | |||
| площадь под кривой уменьшается |
Решение:
Полная вероятность равна: 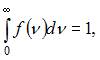 то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 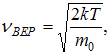 при которой функция
при которой функция 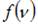 максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 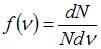 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 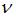 до
до 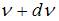 в расчете на единицу этого интервала.
в расчете на единицу этого интервала.
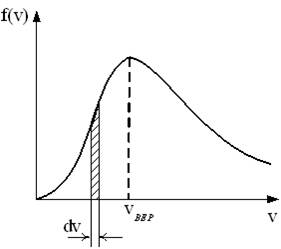
Если, не меняя температуры взять другой газ с меньшей молярной массой и таким же числом молекул, то:
 | максимум кривой сместится вправо в сторону больших скоростей | ||
 | площадь под кривой не изменится | ||
| высота максимума увеличится | |||
| площадь под кривой уменьшится |
Решение:
Функция Максвелла имеет вид 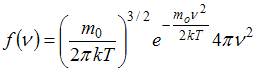 .
.
Полная вероятность равна: 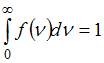 , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры или массы молекул не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры или массы молекул не изменяется. Из формулы наиболее вероятной скорости 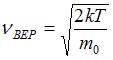 , при которой функция
, при которой функция 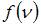 максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при уменьшении массы молекул газа максимум функции сместится вправо, следовательно, высота максимума уменьшится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при уменьшении массы молекул газа максимум функции сместится вправо, следовательно, высота максимума уменьшится.
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 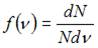 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 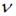 до
до 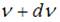 в расчете на единицу этого интервала.
в расчете на единицу этого интервала.

Для этой функции верным является утверждение, что при понижении температуры:
 | наиболее вероятная скорость молекул уменьшается | ||
| величина максимума функции уменьшается | |||
| площадь под кривой уменьшается | |||
| максимум кривой смещается вправо |
Решение:
Полная вероятность равна: 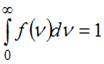 , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 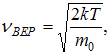 при которой функция
при которой функция 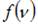 максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 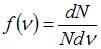 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 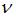 до
до 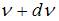 в расчете на единицу этого интервала:
в расчете на единицу этого интервала:
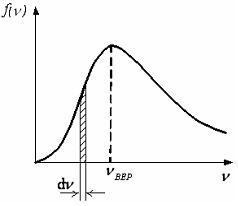
Для этой функции верными являются утверждения:
 | положение максимума кривой зависит не только от температуры, но и от природы газа (его молярной массы) | ||
 | при увеличении числа молекул площадь под кривой не изменяется | ||
| с ростом температуры газа значение максимума функции увеличивается | |||
| для газа с большей молярной массой (при той же температуре) максимум функции расположен в области больших скоростей |
Решение:
Из определения функции распределения Максвелла следует, что выражение 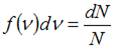 определяет долю молекул, скорости которых заключены в интервале скоростей от
определяет долю молекул, скорости которых заключены в интервале скоростей от 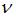 до
до 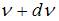 (на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна
(на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна 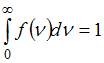 и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости
и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости 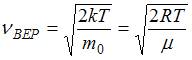 (при которой функция
(при которой функция 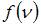 максимальна) следует, что
максимальна) следует, что 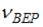 прямо пропорциональна
прямо пропорциональна 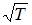 и обратно пропорциональна
и обратно пропорциональна 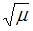 , где
, где 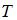 и
и 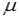 – температура и молярная масса газа соответственно.
– температура и молярная масса газа соответственно.
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 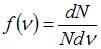 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 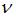 до
до 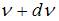 в расчете на единицу этого интервала:
в расчете на единицу этого интервала:

Для этой функции верными являются утверждения:
 | с увеличением температуры максимум кривой смещается вправо | ||
 | площадь заштрихованной полоски равна доле молекул со скоростями в интервале от 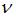 до до 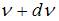 | ||
| с ростом температуры значение максимума функции увеличивается | |||
| с ростом температуры площадь под кривой увеличивается |
Решение:
Из определения функции распределения Максвелла следует, что выражение 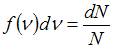 определяет долю молекул, скорости которых заключены в интервале скоростей от
определяет долю молекул, скорости которых заключены в интервале скоростей от 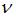 до
до 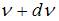 (на графике – площадь заштрихованной полоски). Тогда площадь под кривой равна
(на графике – площадь заштрихованной полоски). Тогда площадь под кривой равна 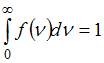 и не изменяется при изменении температуры. Из формулы наиболее вероятной скорости
и не изменяется при изменении температуры. Из формулы наиболее вероятной скорости 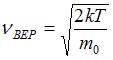 (при которой функция
(при которой функция 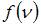 максимальна) следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
максимальна) следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 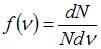 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 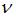 до
до 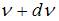 в расчете на единицу этого интервала:
в расчете на единицу этого интервала:

Для этой функции верными являются утверждения:
 | положение максимума кривой зависит не только от температуры, но и от природы газа (его молярной массы) | ||
 | при увеличении числа молекул площадь под кривой не изменяется | ||
| с ростом температуры газа значение максимума функции увеличивается | |||
| для газа с большей молярной массой (при той же температуре) максимум функции расположен в области больших скоростей |
Решение:
Из определения функции распределения Максвелла следует, что выражение 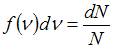 определяет долю молекул, скорости которых заключены в интервале скоростей от
определяет долю молекул, скорости которых заключены в интервале скоростей от 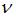 до
до 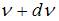 (на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна
(на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна 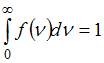 и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости
и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости 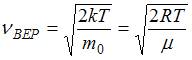 (при которой функция
(при которой функция 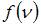 максимальна) следует, что
максимальна) следует, что 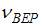 прямо пропорциональна
прямо пропорциональна 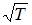 и обратно пропорциональна
и обратно пропорциональна 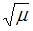 , где
, где 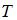 и
и 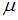 – температура и молярная масса газа соответственно.
– температура и молярная масса газа соответственно.
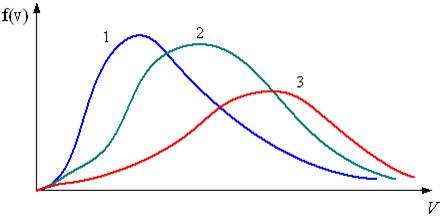
В трех сосудах находятся газы, причем для температур и масс молекул газов имеют место следующие соотношения: 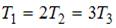 ,
, 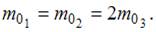 На рисунке схематически представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла) для этих газов, где
На рисунке схематически представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла) для этих газов, где 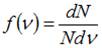 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 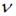 до
до 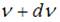 в расчете на единицу этого интервала:
в расчете на единицу этого интервала:
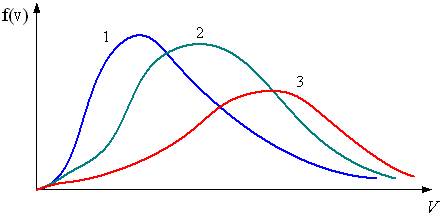
Для графиков этих функций верными являются утверждения, что:
 | кривая 1 соответствует распределению по скоростям молекул газа в сосуде 2 | ||
 | кривая 3 соответствует распределению по скоростям молекул газа в сосуде 1 | ||
| кривая 2 соответствует распределению по скоростям молекул газа в сосуде 2 | |||
| кривая 3 соответствует распределению по скоростям молекул газа в сосуде 3 |
Решение:
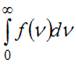 имеет смысл площади, ограниченной кривой распределения и осью абсцисс, и численно равен доле молекул, скорости которых имеют всевозможные значения от 0 до
имеет смысл площади, ограниченной кривой распределения и осью абсцисс, и численно равен доле молекул, скорости которых имеют всевозможные значения от 0 до  . Так как этому условию удовлетворяют все
. Так как этому условию удовлетворяют все  молекул, то
молекул, то 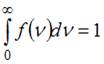 и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 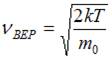 , при которой функция
, при которой функция 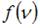 максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. При увеличении массы молекул значение наиболее вероятной скорости уменьшается, следовательно, максимум функции сместится влево и высота максимума увеличится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. При увеличении массы молекул значение наиболее вероятной скорости уменьшается, следовательно, максимум функции сместится влево и высота максимума увеличится.
В трех одинаковых сосудах при равных условиях находится одинаковое количество водорода, гелия и азота

На рисунке представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла), где 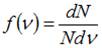 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 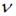 до
до 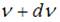 в расчете на единицу этого интервала.
в расчете на единицу этого интервала.

Для этих функций верными являются утверждения, что:
 | кривая 1 соответствует распределению по скоростям молекул азота | ||
 | кривая 3 соответствует распределению по скоростям молекул водорода | ||
| кривая 1 соответствует распределению по скоростям молекул гелия | |||
| кривая 2 соответствует распределению по скоростям молекул азота |
Решение:
Функция Максвелла имеет вид 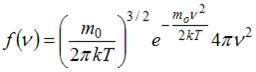 .
.
Полная вероятность равна: 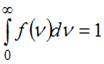 , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 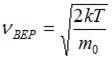 , при которой функция
, при которой функция 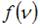 максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится. Наибольшая масса молекул у азота, меньше у гелия и еще меньше у водорода.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится. Наибольшая масса молекул у азота, меньше у гелия и еще меньше у водорода.
В трех одинаковых сосудах находится одинаковое количество газа, причем 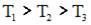

На рисунке представлены графики функций распределения молекул идеального газа по скоростям (распределение Максвелла), где 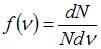 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 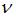 до
до 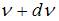 в расчете на единицу этого интервала.
в расчете на единицу этого интервала.
Для этих функций верными являются утверждения, что:
 | кривая 1 соответствует распределению по скоростям молекул газа при температуре 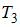 | ||
 | кривая 3 соответствует распределению по скоростям молекул газа при температуре 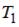 | ||
кривая 2 соответствует распределению по скоростям молекул газа при температуре 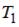 | |||
кривая 3 соответствует распределению по скоростям молекул газа при температуре 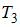 |
Решение:
Полная вероятность равна: 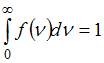 , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 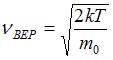 , при которой функция
, при которой функция 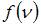 максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится.
На рисунке представлены графики функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 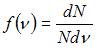 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 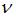 до
до 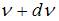 в расчете на единицу этого интервала.
в расчете на единицу этого интервала.
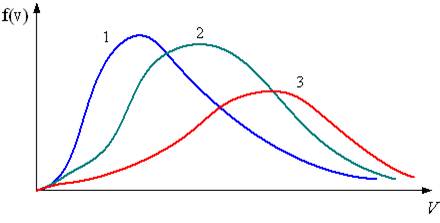
Для этих функций верными являются утверждения, что:
 | распределение 1 соответствует газу, имеющему наибольшую массу молекул (при одинаковой температуре) | ||
| распределение 2 соответствует газу, имеющему наибольшую температуру (при одинаковой массе) | |||
| распределение 1 соответствует газу, имеющему наименьшую массу молекул (при одинаковой температуре) | |||
| распределение 3 соответствует газу, имеющему наименьшую температуру (при одинаковой массе) |
Решение:
Функция Максвелла имеет вид 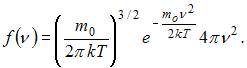
Полная вероятность равна: 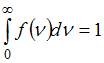 , то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости
, то есть площадь, ограниченная кривой распределения Максвелла, равна единице и при изменении температуры не изменяется. Из формулы наиболее вероятной скорости 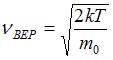 , при которой функция
, при которой функция 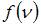 максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится.
максимальна, следует, что при повышении температуры максимум функции сместится вправо, следовательно, высота максимума уменьшится. Если сравнивать распределения Максвелла по скоростям различных газов при одной и той же температуре, то при увеличении массы молекулы газа максимум функции сместится влево, следовательно, высота максимума увеличится.
Зависимости давления p идеального газа во внешнем однородном поле силы тяжести от высоты h для двух разных температур представлены на рисунке.
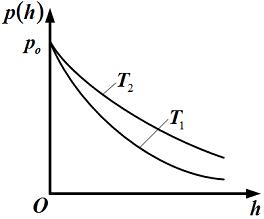
Для графиков этих функций верным является утверждение, что …
 | температура 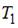 ниже температуры ниже температуры 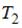 | ||
давление газа на высоте h равно давлению на «нулевом уровне» 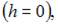 если температура газа стремится к абсолютному нулю если температура газа стремится к абсолютному нулю | |||
температура 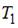 выше температуры выше температуры 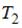 | |||
| зависимость давления идеального газа от высоты не зависит от массы молекул |
Решение:
Зависимость давления идеального газа от высоты 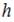 для некоторой температуры
для некоторой температуры 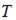 определяется барометрической формулой:
определяется барометрической формулой: 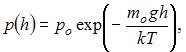 где
где 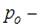 давление на высоте
давление на высоте 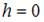 ,
, 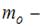 масса молекулы,
масса молекулы, 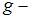 ускорение свободного падения,
ускорение свободного падения, 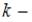 постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура T. Давление
постоянная Больцмана. Из формулы следует, что при постоянной температуре давление газа уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура T. Давление 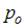 определяется весом всего газа и не меняется при изменении температуры.
определяется весом всего газа и не меняется при изменении температуры.
Формула 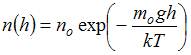 описывает распределение одинаковых молекул массой
описывает распределение одинаковых молекул массой 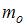 по высоте в изотермической атмосфере; здесь
по высоте в изотермической атмосфере; здесь 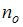 – концентрация молекул при
– концентрация молекул при 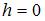 ,
, 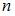 – их концентрация на высоте
– их концентрация на высоте 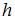 . Для этой зависимости справедливы следующие утверждения:
. Для этой зависимости справедливы следующие утверждения:
 | приведенные на рисунке кривые соответствуют распределениям для одного и того же газа при разных температурах, причем 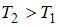 : : 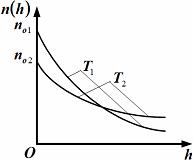 | ||
 | приведенные на рисунке кривые соответствуют распределениям для двух разных газов при одинаковой температуре, причем массы молекул удовлетворяют соотношению 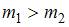 : : 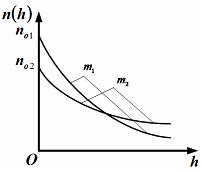 | ||
приведенные на рисунке кривые соответствуют распределениям для одного и того же газа при разных температурах, причем  : :  | |||
приведенные на рисунке кривые соответствуют распределениям для двух разных газов при одинаковой температуре, причем массы молекул удовлетворяют соотношению   |
Решение:
Зависимость концентрации молекул идеального газа от высоты 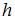 для некоторой температуры
для некоторой температуры 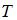 определяется распределением Больцмана:
определяется распределением Больцмана: 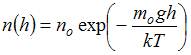 , где
, где 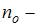 концентрация молекул на высоте
концентрация молекул на высоте 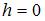 ,
, 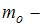 масса молекулы,
масса молекулы, 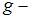 ускорение свободного падения,
ускорение свободного падения, 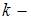 постоянная Больцмана. Из формулы следует, что концентрация газа уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, вследствие теплового движения более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне»
постоянная Больцмана. Из формулы следует, что концентрация газа уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, вследствие теплового движения более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» 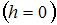 меньше, чем для более тяжелых молекул (при одинаковом общем количестве молекул). Для молекул, имеющих б?льшую массу, скорость изменения концентрации выше. С другой стороны для одного и того же газа чем выше температура, тем выше интенсивность хаотического теплового движения, и концентрация молекул газа на «нулевом уровне»
меньше, чем для более тяжелых молекул (при одинаковом общем количестве молекул). Для молекул, имеющих б?льшую массу, скорость изменения концентрации выше. С другой стороны для одного и того же газа чем выше температура, тем выше интенсивность хаотического теплового движения, и концентрация молекул газа на «нулевом уровне» 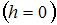 меньше концентрации тех же молекул при более низкой температуре. При этом скорость уменьшения концентрации при увеличении высоты при боле высокой температуре ниже, то есть экспоненциальный спад более пологий.
меньше концентрации тех же молекул при более низкой температуре. При этом скорость уменьшения концентрации при увеличении высоты при боле высокой температуре ниже, то есть экспоненциальный спад более пологий.
На рисунке представлены графики зависимости концентрации молекул идеального газа n от высоты h над уровнем моря для двух разных температур –  (распределение Больцмана).
(распределение Больцмана).
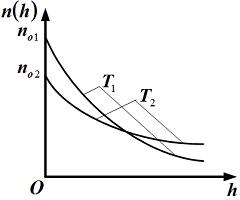
Для графиков этих функций верным является утверждение, что:
 | температура 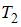 выше температуры выше температуры 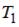 | ||
| с понижением температуры молекулы более равномерно распределяются по высоте | |||
температура 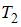 ниже температуры ниже температуры 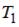 | |||
концентрация молекул газа на «нулевом уровне» 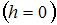 с повышением температуры увеличивается с повышением температуры увеличивается |
Решение:
Зависимость концентрации молекул идеального газа от высоты 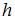 для некоторой температуры
для некоторой температуры 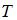 определяется распределением Больцмана:
определяется распределением Больцмана: 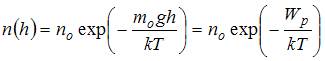 , где
, где 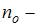 концентрация молекул на высоте
концентрация молекул на высоте 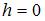 ,
, 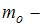 масса молекулы,
масса молекулы, 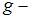 ускорение свободного падения,
ускорение свободного падения, 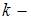 постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул
постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул 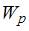 , и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура:
, и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: 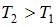 . С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне»
. С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» 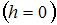 уменьшается, а на высоте
уменьшается, а на высоте 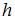 увеличивается.
увеличивается.
На рисунке представлены графики функций распределения молекул идеального газа 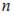 во внешнем однородном поле силы тяжести от высоты
во внешнем однородном поле силы тяжести от высоты 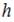 для двух разных газов, где
для двух разных газов, где 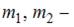 массы молекул газа (распределение Больцмана).
массы молекул газа (распределение Больцмана).
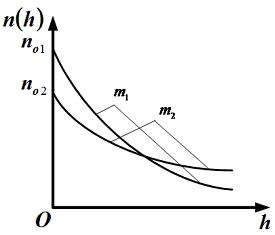
Для этих функций верными являются утверждения, что:
 | масса 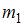 больше массы больше массы 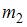 | ||
 | концентрация молекул газа с меньшей массой на «нулевом уровне» 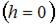 меньше меньше | ||
масса 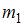 меньше массы меньше массы 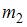 | |||
концентрация молекул газа с меньшей массой на «нулевом уровне» 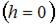 больше больше |
Решение:
Зависимость концентрации молекул идеального газа от высоты 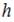 для некоторой температуры
для некоторой температуры 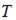 определяется распределением Больцмана:
определяется распределением Больцмана: 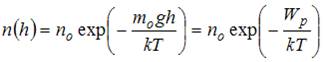 , где
, где 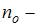 концентрация молекул на высоте
концентрация молекул на высоте  ,
, 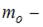 масса молекулы,
масса молекулы, 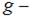 ускорение свободного падения,
ускорение свободного падения, 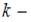 постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул
постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул 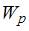 , и уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне»
, и уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» 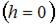 уменьшается, а на высоте
уменьшается, а на высоте 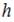 увеличивается.
увеличивается.
Средняя энергия молекул
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 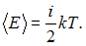 Здесь
Здесь 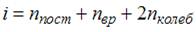 , где
, где 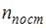 ,
, 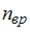 и
и 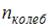 – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место поступательное, вращательное и колебательное движение, для водорода (Н2) число i равно …
– число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место поступательное, вращательное и колебательное движение, для водорода (Н2) число i равно …
 | |||
Решение:
Средняя кинетическая энергия молекулы равна: 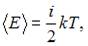 где
где 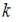 – постоянная Больцмана,
– постоянная Больцмана, 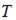 – термодинамическая температура,
– термодинамическая температура, 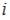 – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: 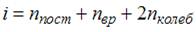 . Для молекулы водорода
. Для молекулы водорода 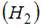 число степеней свободы поступательного движения
число степеней свободы поступательного движения 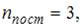 вращательного –
вращательного – 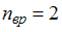 , колебательного –
, колебательного – 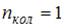 , поэтому
, поэтому 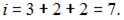
Средняя кинетическая энергия молекулы идеального газа при температуре T равна 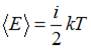 . Здесь
. Здесь 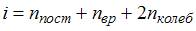 , где
, где 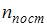 ,
, 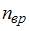 и
и 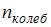 – число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н2O) число i равно …
– число степеней свободы поступательного, вращательного и колебательного движений молекулы. При условии, что имеют место только поступательное и вращательное движение, для водяного пара (Н2O) число i равно …
 | |||
Решение:
Средняя кинетическая энергия молекулы равна: 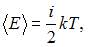 где
где 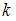 – постоянная Больцмана,
– постоянная Больцмана, 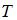 – термодинамическая температура,
– термодинамическая температура, 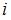 – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: 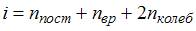 . Для молекулы водяного пара
. Для молекулы водяного пара 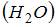 число степеней свободы поступательного движения
число степеней свободы поступательного движения 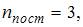 вращательного –
вращательного – 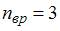 , колебательного –
, колебательного – 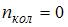 , поэтому
, поэтому 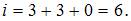
Средняя кинетическая энергия молекул газа при температуре 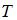 зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекулы водяного пара (
зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекулы водяного пара (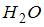 ) равна:
) равна:
 | 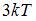 | ||
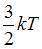 | |||
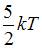 | |||
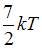 |
Решение:
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная 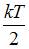 , а на каждую колебательную степень –
, а на каждую колебательную степень – 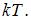 Средняя кинетическая энергия молекулы равна:
Средняя кинетическая энергия молекулы равна: 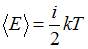 . Здесь
. Здесь 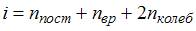 , где
, где 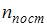 – число степеней свободы поступательного движения,
– число степеней свободы поступательного движения, 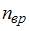 – число степеней свободы вращательного движения,
– число степеней свободы вращательного движения, 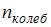 – число степеней свободы колебательного движения. Для молекул идеального газа
– число степеней свободы колебательного движения. Для молекул идеального газа 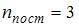 ,
, 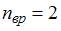 для линейных молекул и
для линейных молекул и 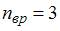 для нелинейных молекул. Молекула водяного пара является нелинейной, поэтому для нее
для нелинейных молекул. Молекула водяного пара является нелинейной, поэтому для нее 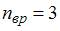 . Поскольку по условию имеет место поступательное и вращательное движение молекулы как целого,
. Поскольку по условию имеет место поступательное и вращательное движение молекулы как целого, 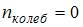 . Таким образом,
. Таким образом, 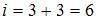 . Тогда средняя энергия молекулы водяного пара (
. Тогда средняя энергия молекулы водяного пара (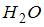 ) равна:
) равна: 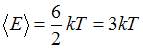 .
.
Если не учитывать колебательные движения в молекуле водорода при температуре 200 К, то кинетическая энергия в (Дж) всех молекул в 4 г водорода равна:
 | 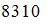 | ||
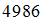 | |||
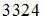 | |||
 |
Решение:
Средняя кинетическая энергия одной молекулы равна: 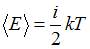 , где
, где 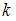 – постоянная Больцмана,
– постоянная Больцмана, 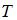 – термодинамическая температура;
– термодинамическая температура; 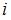 – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы
– сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы 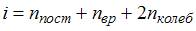 . Молекула водорода
. Молекула водорода 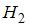 имеет 3 поступательные и 2 вращательные степени свободы, следовательно,
имеет 3 поступательные и 2 вращательные степени свободы, следовательно, 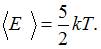 В 4 г водорода содержится
В 4 г водорода содержится 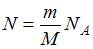 молекул, где
молекул, где 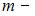 масса газа,
масса газа, 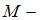 молярная масса водорода,
молярная масса водорода, 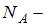 число Авогадро. Кинетическая энергия всех молекул будет равна:
число Авогадро. Кинетическая энергия всех молекул будет равна: 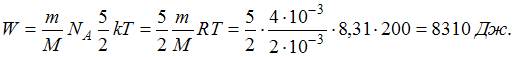
Газ занимает объем 5 л под давлением 2 МПа. При этом кинетическая энергия поступательного движения всех его молекул равна:
 | 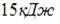 | ||
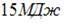 | |||
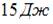 | |||
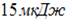 |
Решение:
Согласно уравнению кинетической теории для давления идеального газа (основному уравнению МКТ идеальных газов), произведение давления идеального газа и его объема равно двум третям энергии поступательного движения всех его молекул: 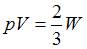 . Отсюда
. Отсюда 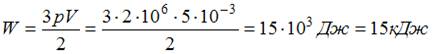 .
.
В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: 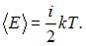 Здесь
Здесь 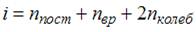 , где
, где 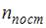 ,
, 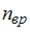 и
и 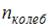 – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно.
– число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно.
Для гелия (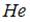 ) средняя кинетическая энергия молекулы равна:
) средняя кинетическая энергия молекулы равна:
 | 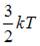 | ||
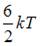 | |||
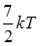 | |||
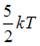 |
Решение:
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная 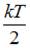 , а на каждую колебательную степень –
, а на каждую колебательную степень – 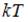 . Средняя кинетическая энергия молекулы равна:
. Средняя кинетическая энергия молекулы равна: 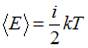 .
.
Здесь 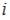 – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: 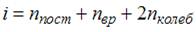 , где
, где 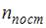 – число степеней свободы поступательного движения, равное 3;
– число степеней свободы поступательного движения, равное 3; 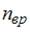 – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;
– число степеней свободы вращательного движения, которое может быть равно 0, 2, 3; 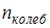 – число степеней свободы колебательного движения, минимальное количество которых равно 1.
– число степеней свободы колебательного движения, минимальное количество которых равно 1.
Для гелия (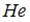 ) (одноатомной молекулы)
) (одноатомной молекулы) 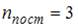 ,
, 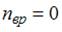 и
и 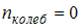 . Следовательно,
. Следовательно, 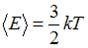 .
.
 2015-02-04
2015-02-04 40169
40169