Отношение средней кинетической энергии вращательного движения к средней энергии молекулы с жесткой связью 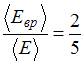 . Это имеет место для …
. Это имеет место для …
 | водорода | ||
| водяного пара | |||
| гелия | |||
метана (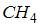 ) ) |
Решение:
Средняя кинетическая энергия молекулы равна: 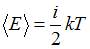 , где
, где 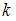 – постоянная Больцмана,
– постоянная Больцмана, 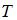 – термодинамическая температура,
– термодинамическая температура, 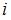 – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: 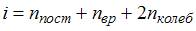 . Средняя энергия вращательного движения
. Средняя энергия вращательного движения 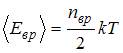 . Таким образом, с учетом того что связь атомов в молекуле по условию является жесткой (в этом случае
. Таким образом, с учетом того что связь атомов в молекуле по условию является жесткой (в этом случае 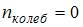 ), отношение
), отношение 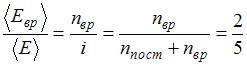 . Отсюда
. Отсюда 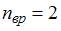 , что имеет место для газов с двухатомными и многоатомными линейными молекулами. Следовательно, это – водород.
, что имеет место для газов с двухатомными и многоатомными линейными молекулами. Следовательно, это – водород.
Тема: Средняя энергия молекул
При комнатной температуре отношение 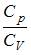 молярных теплоемкостей при постоянном давлении и постоянном объеме равно
молярных теплоемкостей при постоянном давлении и постоянном объеме равно 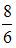 для …
для …
 | водяного пара | ||
| гелия | |||
| воздуха | |||
| кислорода |
Решение:
Из отношения 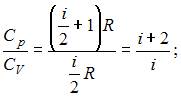
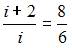 найдем
найдем 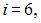
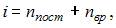
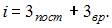 3 поступательные и 3 вращательные степени свободы имеют трехатомные и многоатомные газы, следовательно, это водяной пар.
3 поступательные и 3 вращательные степени свободы имеют трехатомные и многоатомные газы, следовательно, это водяной пар.
Тема: Средняя энергия молекул
При комнатной температуре коэффициент Пуассона 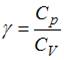 , где
, где 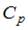 и
и 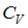 – молярные теплоемкости при постоянном давлении и постоянном объеме соответственно, равен
– молярные теплоемкости при постоянном давлении и постоянном объеме соответственно, равен 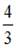 для …
для …
 | водяного пара | ||
| водорода | |||
| азота | |||
| гелия |
Решение:
Из отношения 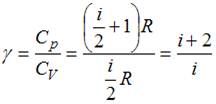 . При комнатной температуре
. При комнатной температуре 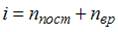 , где
, где 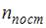 и
и 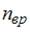 – число поступательных и вращательных степеней свободы. По условию
– число поступательных и вращательных степеней свободы. По условию 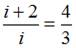 . Отсюда
. Отсюда 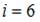 . Так как для молекул газа
. Так как для молекул газа 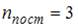 , то для рассматриваемого газа
, то для рассматриваемого газа 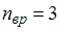 , а три вращательные степени свободы имеют трехатомные и многоатомные газы с нелинейными молекулами. Следовательно, речь идет о водяном паре.
, а три вращательные степени свободы имеют трехатомные и многоатомные газы с нелинейными молекулами. Следовательно, речь идет о водяном паре.
Тема: Средняя энергия молекул
В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: 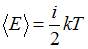 . Здесь
. Здесь 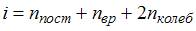 , где
, где 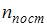 ,
, 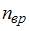 и
и 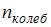 – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для азота
– число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для азота 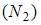 средняя кинетическая энергия колебательного движения молекулы равна …
средняя кинетическая энергия колебательного движения молекулы равна …
 | 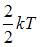 | ||
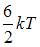 | |||
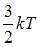 | |||
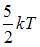 |
Решение:
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная 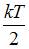 , а на каждую колебательную степень свободы –
, а на каждую колебательную степень свободы – 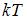 . Средняя кинетическая энергия молекулы равна:
. Средняя кинетическая энергия молекулы равна: 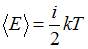 .
.
Здесь 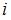 – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: 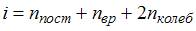 , где
, где 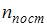 – число степеней свободы поступательного движения, равное 3;
– число степеней свободы поступательного движения, равное 3; 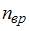 – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;
– число степеней свободы вращательного движения, которое может быть равно 0, 2, 3; 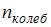 – число степеней свободы колебательного движения, минимальное количество которых равно 1.
– число степеней свободы колебательного движения, минимальное количество которых равно 1.
Для азота (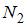 ) (двухатомной молекулы)
) (двухатомной молекулы) 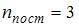 ,
, 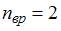 и
и 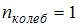 . Следовательно,
. Следовательно, 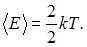
Тема: Средняя энергия молекул
При комнатной температуре отношение 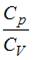 молярных теплоемкостей при постоянном давлении и постоянном объеме равно
молярных теплоемкостей при постоянном давлении и постоянном объеме равно 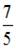 для …
для …
 | кислорода | ||
| водяного пара | |||
| углекислого газа | |||
| гелия |
Тема: Средняя энергия молекул
Молярная теплоемкость идеального газа при постоянном давлении равна 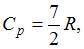 где
где 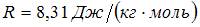 – универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно …
– универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно …
 | |||
Решение:
Молярная теплоемкость идеального газа в изобарном процессе определяется соотношением 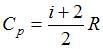 , где
, где 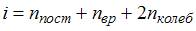 . Здесь
. Здесь 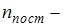 число степеней свободы поступательного движения;
число степеней свободы поступательного движения; 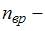 число степеней свободы вращательного движения;
число степеней свободы вращательного движения; 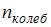 – число степеней свободы колебательного движения. Для молекул идеального газа
– число степеней свободы колебательного движения. Для молекул идеального газа 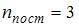 ,
, 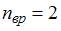 для линейных молекул и
для линейных молекул и 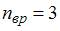 для нелинейных молекул. Из сопоставления с данными задания следует, что
для нелинейных молекул. Из сопоставления с данными задания следует, что 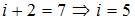 . С учетом того что
. С учетом того что 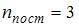 , приходим к выводу, что
, приходим к выводу, что 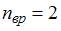 . В данном случае
. В данном случае 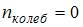 .
.
Тема: Первое начало термодинамики. Работа при изопроцессах
Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты 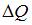 . На увеличение внутренней энергии газа расходуется часть теплоты
. На увеличение внутренней энергии газа расходуется часть теплоты 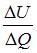 , равная …
, равная …
 | 0,6 | ||
| 1,7 | |||
| 0,7 | |||
| 1,4 |
Решение:
Изменение внутренней энергии газа равно 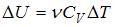 . Количество теплоты, переданное газу при изобарическом процессе, можно определить по формуле
. Количество теплоты, переданное газу при изобарическом процессе, можно определить по формуле 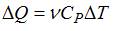 . Тогда
. Тогда 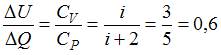 , где
, где 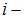 число степеней свободы молекулы, для одноатомного газа
число степеней свободы молекулы, для одноатомного газа 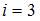 .
.
 2015-02-04
2015-02-04 7859
7859
