Лекция 8. Аналитические методы определения характеристик тепловых объектов

Содержание лекции:

- аналитические методы моделирования тепловых объектов с сосредоточенными параметрами..

Цель лекции:

- изучить на примерах основные методы аналитического моделирования тепловых объектов с сосредоточенными параметрами.

Рассмотрим конкретные теплоэнергетические объекты. Исходными уравнениями являются приведенные выше уравнения материального и теплового баланса.

Пример 8.1.Необогреваемый участок парогенератора (коллектор, соединительный паропровод). Входная величина – температура среды на входе в участок, выходная - температура среды на выходе из участка. Давление среды в участке предполагается постоянным, отвод тепла в окружающую среду отсутствует.

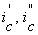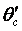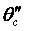Примем обозначения: D_c – расход среды; – энтальпия среды на входе и выходе; Q_м – тепловой поток к металлу участка; I_c – энтальпия среды участка; I_м – энтальпия металла участка; G_c и G_м – масса среды и металла на участке; i_м – энтальпия металла; α₂ – коэффициент теплоотдачи на внутреннюю поверхность H₂ участка; и – температура среды на входе и выходе участка; 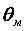– температура металла; с_р и с_м – удельные теплоемкости среды и металла.

Уравнение теплового баланса для рабочей среды:

.

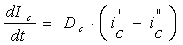Уравнение теплового баланса для металла:

.

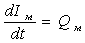Учитывая, что I_c = i’’_c· G_c, I_м = i_м· G_м, Q_м = α₂·H₂· (Θ’’_c - Θ_м), ∆i = с·∆ Θ,

после перехода к отклонениям переменных и вычитания уравнений стационарного режима, получим дифференциальные уравнения для линейной модели участка:

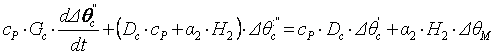(8.1) . (8.2)

Преобразуем по Лапласу уравнения (8.1), (8.2). Для этого обе части уравнения умножим на e^-st и проинтегрируем от 0 до ∞, имея ввиду, что изображения функции и ее производной (при нулевых начальных условиях) связаны следующим свойством

y(t)÷Y(s), y'(t)÷sY(s).

Примем ∆Θ’’_c ÷ Z(s), ∆Θ’_c ÷Y(s), ∆Q_м ÷X(s). Тогда

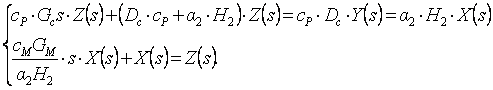Из второго уравнения: .

Из первого уравнения:

.

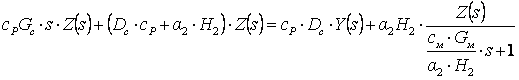Разделим на D_cc_p. Получим

.

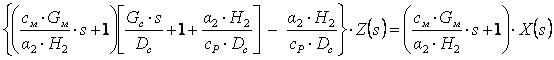Отсюда .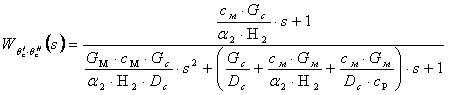

Постоянная времени 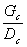физически соответствует времени заполнения средой участка при данном расходе среды и обычно мала. В практических расчетах ее принимают равной 0, и передаточная функция принимает более простое выражение:

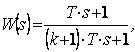где .

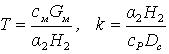Пример 8.2.Теплообменник смешения (коллектор впрыска). Входными переменными являются расход и температура среды на входе, расход впрыскиваемой воды; выходная величина – температура среды на выходе. Расход среды на выходе равен сумме расходов среды на входе и расхода среды на впрыск, температура впрыскиваемой воды предполагается постоянной.

Уравнение теплового баланса для рабочей среды

где 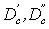- расход среды на входе и выходе участка, 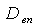- расход воды на впрыск, 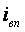- энтальпия впрыскиваемой воды.

Аналогично предыдущему после перехода к отклонениям переменных и вычитания уравнения стационарного режима получим линейное дифференциальное уравнение для рабочей среды

(8.3)

где 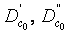- расход среды на входе и выходе участка в стационарном режиме, 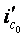- энтальпия среды на входе участка в стационарном режиме, 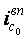- энтальпия впрыскиваемой воды в стационарном режиме.

Для металла сохраняется в силе уравнение (8.2).

Из уравнений (8.2) (8.3) после преобразований по Лапласу и аналогичных предыдущему упрощений получим передаточные функции по различным каналам:

а) найдем передаточную функцию по каналу 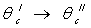: 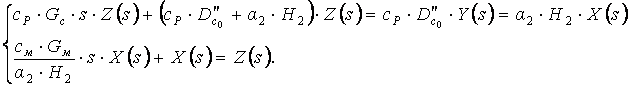Отсюда

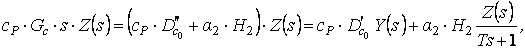
где .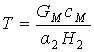

Поделив на 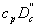и принимая, что постоянная времени 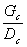мала, имеем:

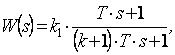где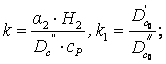

б) передаточная функция по каналу

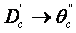равна где ;

в) по каналу

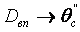равна где .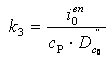

Пример 8.3. Паровая емкость. Предполагается, что сопротивление емкости сосредоточено на ее выходе и энтальпия среды в переходном процессе остается без изменения. Давление среды за емкостью поддерживается постоянным с помощью регулятора, задание которому может изменяться. Изменение давления среды в емкости не влияет на расход подводимого вещества. Входными величинами являются расход среды на входе и давление среды на выходе, выходными – расход среды на выходе и давление в емкости.

Уравнение материального баланса для среды

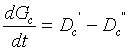. (8.4)

Расход среды через сосредоточенное сопротивление определяется выражением

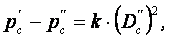(8.5)

где 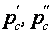- давление среды перед сопротивлением и за ним.

После перехода к отклонениям переменных и линеаризации с учетом, что G_c =ρ_c ·V и , получим уравнения линейной модели системы

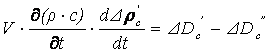; (8.6)

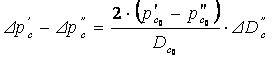(8.7)

где V - объем среды в участке, ρ_c - плотность среды, 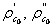- давление среды перед и за сопротивлением в стационарном режиме, 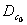- расход среды в стационарном режиме.

После преобразования по Лапласу из последних уравнений можно получить передаточные функции по каналам

, ,

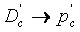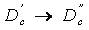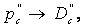
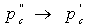
(рекомендуется студентам получить самостоятельно).