Краткие сведения об аппроксимации функций

Задача аппроксимации – это задача приближения функции по какой-либо системе функций. Пусть рассматриваемая функция f(t) абсолютно интегрируема на интервале [0,T]. На практике это требование, обычно, выполняется. Эта функция разлагается по некоторой системе аппроксимирующих функций {φ(t)}, абсолютно интегрируемых на том же интервале времени

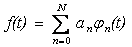. (17.1)

Вид системы аппроксимирующих функций выбирается исходя из априорной информации об аппроксимируемой функции. Коэффициенты аппроксимации выбираются таким образом, чтобы минимизировать некоторый заранее выбранный критерий приближения. Можно воспользоваться одним из следующих видов приближения: равномерным, интерполяционным, квадратичным. Для точного решения задачи с использованием двух первых видов приближения не существует конечного алгоритма для вычисления коэффициентов разложения на бесконечном интервале (который чаще всего входит в алгоритмы идентификации). Это обстоятельство, а также алгоритмическая простота реализации квадратичных приближений обусловили их широкое распространение. Коэффициенты разложения в этом случае могут быть получены из системы алгебраических уравнений. Вводя обозначения для скалярных произведений

(17.2)

получим искомую систему:

a₀(φ₀, φ₀) + a₁(φ₀, φ₁) + … + a_N(φ₀, φ_N) = (φ₀, f);

………………………………………………… (17.3)

a₀(φ₀, φ_N) + a₁(φ₁, φ_N) + … + a_N(φ_N, φ_N) = (φ_N, f).

Условием единственности решения системы (17.3) является неравенство нулю ее определителя. Определитель не равен нулю тогда и только тогда, когда выбранная система аппроксимирующих функций является линейно-независимой.

Если не предъявлять к аппроксимирующей системе функций больше никаких требований (кроме абсолютной интегрируемости), система (17.3) решается совместно. И при изменении длины отрезка N нужно заново вычислять все коэффициенты a_n. Кроме того, для решения системы надо определить N(N+1)/2 интегралов вида (17.2). Для достижения независимости определения коэффициентов аппроксимации a_n и упрощения решения системы (17.3) функции {φ(t)} целесообразно выбрать ортогональными на интервале [0,T], то есть удовлетворяющими условию

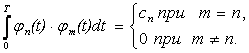(17.4)

где c_n - некоторая постоянная.

Если функции {φ(t)} ортогональны, определитель системы (17.3) становится диагональным и формулы для вычисления коэффициентов упрощаются до вида

.

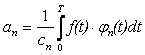Если постоянныеc_n=1, система функций {φ(t)} является ортонормированной, выражения для формул упрощаются до вида широко известных формул Фурье, а сами коэффициенты в этом случае называются коэффициентами Фурье (по аналогии с рядом Фурье, члены которого также представляют собой ортонормированные на [0,T] функции. Иногда выбирают функции, ортогональные с некоторым весом w(t)

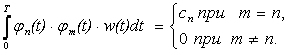. (17.5)

Функция веса выбирается таким образом, чтобы выделить ошибку на интересующем интервале изменения независимой переменной.

Недостатком рассмотренного выше алгебраического метода является необходимость решения системы Винера-Хопфа.Некорректность исходного интегрального уравнения приводит к плохой обусловленности этой системы. Есть несколько способов получения плавной импульсной переходной функции, которые выбираются на основе имеющейся априорной информации об объекте.