Сглаживание дискретных значений импульсной переходной функции

Наиболее простой и появившейся ранее других формой сглаживания является аппроксимация полученного решения системы алгебраических уравнений, эквивалентных уравнению Винера-Хопфа.

В результате решения системы уравнений (16.5) численным методом, получим дискретные значения g₀, g₁,…, g_mимпульсной переходной функции g(t) в равноотстоящих точках 0, 1,…, n. Полученную последовательность дискретных величин представим с помощью какого-либо аппроксимирующего полинома

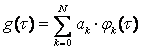(17.6)

где {φ_k(τ)}- какая-либо система аппроксимирующих ортогональных функций.

Коэффициенты аппроксимации определяются как

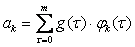. (17.7)

Основные требования, предъявляемые к аппроксимирующей системе функций:

- функции {φ_k(τ)}должны быть абсолютно интегрируемы;

- функции {φ_k(τ)}должны быть достаточно гладкими для регуляризации решения уравнения идентификации;

- система функций {φ_k(τ)} должна быть линейно-независимой;

- система функций {φ_k(τ)} должна быть ортогональной;

- система функций {φ_k(τ)} должна гарантировать быстроту

аппроксимации с ростом степени полинома N;

- функции {φ_k(τ)} должны быть просто реализуемы с помощью

несложных вычислений.

Возникает вопрос о выборе степени Nаппроксимирующего полинома. Этот вопрос очень сложен и в настоящее время не решен до конца. При решении этой задачи возможны следующие подходы:

1. В ряде случаев характер импульсной переходной функции известен. Это позволяет определить степень Nаппроксимирующего полинома (17.6) с учетом конкретного вида аппроксимирующих функций {φ_k(τ)}.

2. Если известна дисперсия ошибки измерения взаимно-корреляционной функции R_yx значениеN можно определить по широко принятому в математической статистике критерию χ².

3. Если дисперсия ошибки измерения R_yxнеизвестна, значение Nможно определить по известному из математической статистики критерию Фишера.

Однако следует отметить, что при больших значениях N в силу ошибок вычисления критерии Пирсона и Фишера становятся малонадежными.

4. Довольно общий подход к определению степени аппроксимирующего полинома N основан на принципе Гаусса. Значение N находится из условия минимума по N функционала

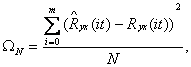(17.8)

где 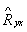- результат подстановки полинома (17.7) в систему уравнений (17.6) вместо импульсной переходной функции g(t). То есть минимизируется дисперсия R_yх.