Алгебраический метод решения уравнения Винера-Хопфа

Один из методов решения уравнения (16.4) – алгебраический. Представим (16.4) в виде системы линейных алгебраических уравнений. Для этого перейдем к дискретному времени, интеграл запишем в виде суммы. Интервал разбивается на mравных интервалов t, 2t, …, mt и интегралзаписываетсяприближенно в виде суммы:

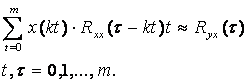(16.5)

Обозначим g_i =g(it) и полагая τ = t, 2t,..., mt, получим систему:

R_x·G=Q (16.6)

где G = [g₁, g₂,…,g_m]^T, Q= [q₁, q₂…, q_m]^T, ,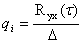

R_x – квадратная симметричная матрица mхm:

.

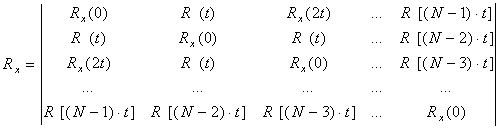Таким образом, получили систему mлинейных уравнений для определения mзначений ординат весовой функции g(τ) в точках t, 2t,…, mt.

В реальных объектах обычно g(0) = 0, поэтому в правых частях уравнений (16.6) можно убрать первые слагаемые. Кроме того, чтобы сохранить диагональную симметричность определителя системы, часто 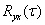сдвигают на один шаг, то есть систему (16.6) рассматривают не с первой строки, а со второй. Если отрезок ∆ достаточно мал, ошибка будет незначительна.

Уравнение Винера-Хопфа является плохо обусловленным: даже малые вариации в исходных значениях корреляционных функций приводят к большим вариациям решений. К тому же вместо истинных значений корреляционных функций использовались их оценки. Поэтому решение уравнения Винера-Хопфа получается с большими погрешностями. Хотя полученные таким образом импульсные переходные функции имеют малую среднеквадратичную ошибку, близкую к минимуму, ценность их невелика, так как эти функции не соответствуют физическому смыслу процессов в объекте. Физический смысл имеют гладкие решения.

Один из методов регуляризации плохо обусловленных уравнений основан на том, что решение ищется в виде линейной комбинации собственных функций интегральных операторов (в случае интегральных уравнений) или собственных чисел линейных операторов (в случае систем линейных алгебраических уравнений). При решении задачи идентификации собственные функции оператора свертки, как правило, неизвестны. Однако, например, разложение решений уравнения Винера-Хопфа по некоторой системе гладких функций, соответствующих реальному протеканию процессов в идентифицируемом объекте, обладает хорошими регуляризующими свойствами. Это относится и к сглаживанию входящих в уравнение Винера-Хопфа корреляционных функций.