Метод идентификации, основанный на предварительной аппроксимации импульсной переходной функции

Более эффективный метод решения задачи идентификации состоит в предварительной аппроксимации импульсной переходной функции объекта g(t) и последующем определении коэффициентов Фурье этого разложения по результатам наблюдений за входными и выходными сигналами. Аппроксимируем импульсную переходную функцию суммой (17.6), где {φ_k(τ)} - ортогональны. Коэффициенты разложения пока неизвестны. Минимизируем отклонение выходных сигналов объекта y(t) и модели y^*(t), где y^*(t)определяется из уравнения свертки

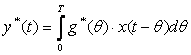. (17.9)

Подставив в это уравнение выражение для импульсной переходной функции (17.6), имеем

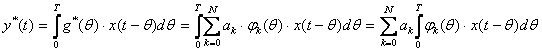(17.10)

Критерий идентификации имеет вид

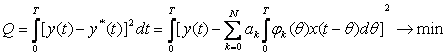. (17.11)

Отсюда

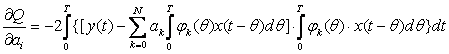. (17.12)

Наилучший выбор имеет место при .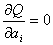

В итоге получим систему

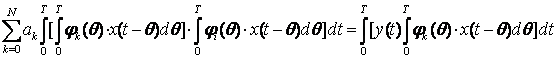(17.13)

для определения неизвестных коэффициентов разложения.

Как правило, на практике N<<m, то есть система (17.13) имеет существенно меньший порядок, чем (16.5) и хорошо обусловлена в силу гладкости системы функций {φ_k(τ)}. Однако проблема выбора степени Nаппроксимирующего полинома остается.