Несобственные интегралы от неограниченных функций

Пусть функция y=f(x) непрерывна, но не ограниченна на полуинтервале .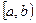

Несобственным интегралом 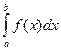от функции y=f(x) на полуинтервале 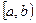называется предел 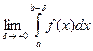, где 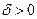, т.е.

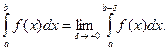. (16)

Если предел, стоящий в правой части равенства (16), существует и конечен, то несобственный интеграл называется сходящимся, в противном случае — расходящимся.

Аналогично вводится понятие несобственного интеграла от функции y=f(x) непрерывной, но неограниченной на .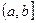

Если функция y=f(x) не ограничена при х=с, где 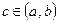, то интеграл 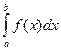также называется несобственным. В этом случае интеграл

= +

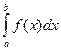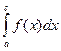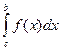
считается сходящимся, если сходятся два несобственных интеграла в правой части равенства. В противном случае 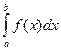называется расходящимся. Например,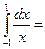 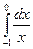+ 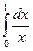является расходящимся, так как расходятся оба несобственных интеграла в правой части равенства.