 Пусть в пространстве задано тело. Пусть построены его сечения плоскостями, перпендикулярными оси
Пусть в пространстве задано тело. Пусть построены его сечения плоскостями, перпендикулярными оси 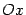 и проходящими через точки x
и проходящими через точки x 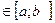 на ней. Площадь фигуры, образующейся в сечении, зависит от точки х, определяющей плоскость сечения. Пусть эта зависимость известна и задана непрерывной на
на ней. Площадь фигуры, образующейся в сечении, зависит от точки х, определяющей плоскость сечения. Пусть эта зависимость известна и задана непрерывной на 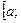
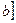 функцией
функцией 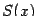 . Тогда объем части тела, находящейся между плоскостями х=а и х=в вычисляется по формуле
. Тогда объем части тела, находящейся между плоскостями х=а и х=в вычисляется по формуле 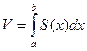
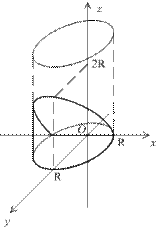
Пример. Найдём объём ограниченного тела, заключённого между поверхностью цилиндра радиуса 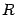 :
: 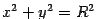 , горизонтальной плоскостью
, горизонтальной плоскостью 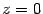 и наклонной плоскостью z=2y и лежащего выше горизонтальной плоскости
и наклонной плоскостью z=2y и лежащего выше горизонтальной плоскости 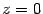 .
.
Очевидно, что рассматриваемое тело 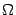 проектируется на ось
проектируется на ось 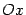 в отрезок
в отрезок  , а при x
, а при x 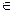
 поперечное сечение тела представляет собою прямоугольный треугольник с катетами y и z=2y, где y можно выразить через x из уравнения цилиндра:
поперечное сечение тела представляет собою прямоугольный треугольник с катетами y и z=2y, где y можно выразить через x из уравнения цилиндра:
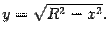
Поэтому площадь S(x) поперечного сечения такова:
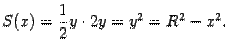
Применяя формулу, находим объём тела 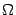 :
:
 2015-02-04
2015-02-04 3006
3006
