При вычислении определенных интегралов широко используется метод замены переменной и метод интегрирования по частям.
Теорема 3. Пусть функция 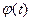 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке 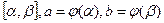 и функция f(x) непрерывна в каждой точке х вида
и функция f(x) непрерывна в каждой точке х вида 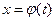 , где
, где 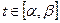 .
.
Тогда справедливо следующее равенство
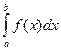 =
= 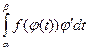 . (11)
. (11)
Формула (11) носит название формулы замены переменной в определенном интеграле.
Использование замены переменной позволяет упростить интеграл, приблизив его к табличному. При этом нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования 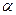 и
и 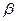 по новой переменной t как решение относительно переменной t уравнений
по новой переменной t как решение относительно переменной t уравнений 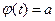 и
и 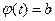 . Часто вместо подстановки
. Часто вместо подстановки 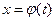 применяют подстановку t=
применяют подстановку t= 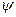 (x). В этом случае нахождение пределов интегрирования по переменной t упрощается:
(x). В этом случае нахождение пределов интегрирования по переменной t упрощается: 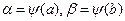 .
.
Пример. Вычислить 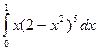 .
.
Положим 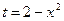 . Тогда
. Тогда 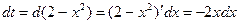 и
и 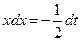 . Если х =0, то
. Если х =0, то 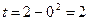 , и если х =1, то
, и если х =1, то 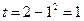 . Следовательно,
. Следовательно,
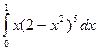 =
= 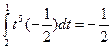
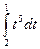 = -
= - 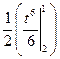 =
=
= - 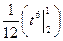 = -
= - 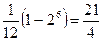 .
.
Рассмотрим теперь, как выполняется интегрирование по частям в определенном интеграле.
Теорема 4. Пусть функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке[ a,b ]. Тогда
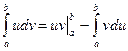 , (12)
, (12)
где 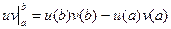 .
.
Формула (12) называется формулой интегрирования по частям для определенного интеграла.
Пример. Вычислить 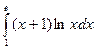 .
.
Пусть u=ln x, dv=(x+1)dx.
Тогда 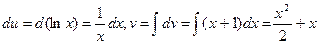 .
.
По формуле (12) имеем
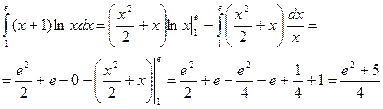
 2015-02-04
2015-02-04 632
632








