1. Явное задание кривой. В этом случае кривая задается в виде 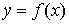 ,
, 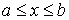 , и длина ее дуги равна L=
, и длина ее дуги равна L= 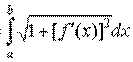 .
.
2. Кривая в полярных координатах. Уравнение кривой имеет в этом случае вид 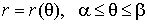 и длина ее дуги равна L=
и длина ее дуги равна L= 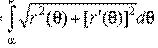 .
.
3. Параметрическое задании кривой. Пусть функции x (t) и y (t) имеют на отрезке 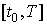 непрерывныепроизводные
непрерывныепроизводные 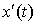 и
и 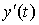 . Тогда длина дуги кривой
. Тогда длина дуги кривой
L= 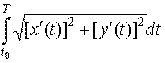 .
.
Пример. Найдём длину дуги кривой (циклоиды), заданной на плоскости 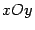 параметрическими уравнениями
параметрическими уравнениями
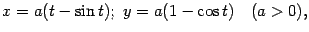
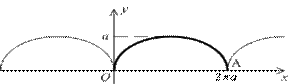 |
лежащей между точками O(0;0) (соответствует
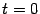 ) и A(2
) и A(2 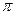 a;0) (соответствует
a;0) (соответствует 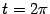 ).
). Для функций f1(t)=a(t-sint) и f2(t)=a(1-cost) вычислим производные: 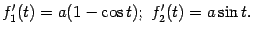
Тогда искомая длина дуги равна
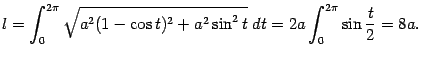
 |
Пример. Пусть линия на плоскости с полярными координатами (r;
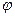 ) задана уравнением r=a
) задана уравнением r=a 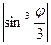 (a>0). Поскольку функция f(
(a>0). Поскольку функция f(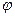 )=a
)=a 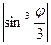 периодична с периодом
периодична с периодом 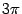 , достаточно рассматривать только значения аргумента
, достаточно рассматривать только значения аргумента 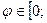
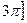 , при которых выражение
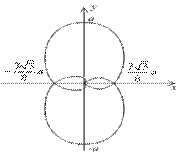
, при которых выражение 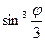 неотрицательно. Кривая имеет вид, изображённый на следующем рисунке.
неотрицательно. Кривая имеет вид, изображённый на следующем рисунке. Найдём длину этой линии.
Имеем 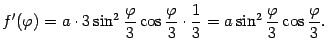
Поэтому искомая длина 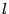 равна
равна
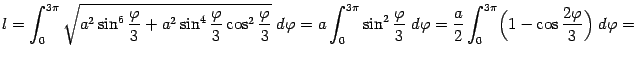
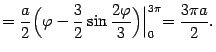
 2015-02-04
2015-02-04 1674
1674








