Назовем длиной свободного пробега молекулы расстояние, которое она проходит между двумя последовательными столкновениями. В результате хаотического движения это расстояние меняется случайным образом. Введем среднюю длину свободного пробега
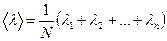 . .
|
|
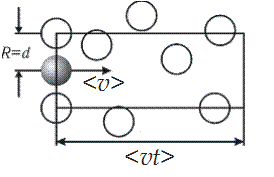 Рис. 8.9.
Рис. 8.9.
|
Для вычисления 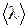 примем упрощенную модель, считая, что все молекулы неподвижны за исключением одной, которая движется со средней скоростью
примем упрощенную модель, считая, что все молекулы неподвижны за исключением одной, которая движется со средней скоростью 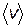 . Будем также считать, что, несмотря на столкновения выделенной нами молекулы с другими, она движется прямолинейно (рис. 8.9). Обозначим через d – диаметр молекулы. Тогда, как видно из рис. 8.9, выделенная молекула столкнется со всеми теми молекулами, центры которых попадают внутрь цилиндра с радиусом R=d. За время t молекула пройдет путь равный
. Будем также считать, что, несмотря на столкновения выделенной нами молекулы с другими, она движется прямолинейно (рис. 8.9). Обозначим через d – диаметр молекулы. Тогда, как видно из рис. 8.9, выделенная молекула столкнется со всеми теми молекулами, центры которых попадают внутрь цилиндра с радиусом R=d. За время t молекула пройдет путь равный 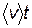 , поэтому объем цилиндра
, поэтому объем цилиндра 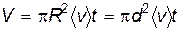 . Если n – число молекул в единице объема, то число молекул, находящихся внутри цилиндра, и, следовательно, и число столкновений за время t
. Если n – число молекул в единице объема, то число молекул, находящихся внутри цилиндра, и, следовательно, и число столкновений за время t
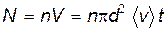 . .
|
|
Среднее число столкновений в единицу времени
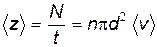 . .
| (8.29)
|
За время t молекула проходит путь, численно равный 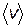 t, испытывая при этом
t, испытывая при этом 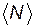 столкновений. Поэтому средняя длина свободного пробега
столкновений. Поэтому средняя длина свободного пробега
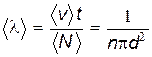 . .
|
|
Учтем теперь движение всех молекул. При таком учете вместо средней скорости движения молекулы 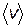 необходимо ввести относительную скорость vотн, равную
необходимо ввести относительную скорость vотн, равную 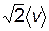 . В результате более точное выражение для длины свободного пробега принимает вид
. В результате более точное выражение для длины свободного пробега принимает вид
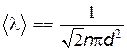 . .
| (8.30)
|
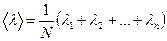 .
.
 Рис. 8.9.
Рис. 8.9.
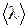 примем упрощенную модель, считая, что все молекулы неподвижны за исключением одной, которая движется со средней скоростью
примем упрощенную модель, считая, что все молекулы неподвижны за исключением одной, которая движется со средней скоростью 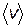 . Будем также считать, что, несмотря на столкновения выделенной нами молекулы с другими, она движется прямолинейно (рис. 8.9). Обозначим через d – диаметр молекулы. Тогда, как видно из рис. 8.9, выделенная молекула столкнется со всеми теми молекулами, центры которых попадают внутрь цилиндра с радиусом R=d. За время t молекула пройдет путь равный
. Будем также считать, что, несмотря на столкновения выделенной нами молекулы с другими, она движется прямолинейно (рис. 8.9). Обозначим через d – диаметр молекулы. Тогда, как видно из рис. 8.9, выделенная молекула столкнется со всеми теми молекулами, центры которых попадают внутрь цилиндра с радиусом R=d. За время t молекула пройдет путь равный 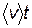 , поэтому объем цилиндра
, поэтому объем цилиндра 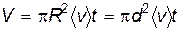 . Если n – число молекул в единице объема, то число молекул, находящихся внутри цилиндра, и, следовательно, и число столкновений за время t
. Если n – число молекул в единице объема, то число молекул, находящихся внутри цилиндра, и, следовательно, и число столкновений за время t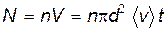 .
.
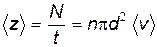 .
.
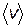 t, испытывая при этом
t, испытывая при этом 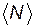 столкновений. Поэтому средняя длина свободного пробега
столкновений. Поэтому средняя длина свободного пробега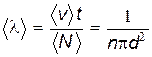 .
.
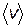 необходимо ввести относительную скорость vотн, равную
необходимо ввести относительную скорость vотн, равную 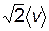 . В результате более точное выражение для длины свободного пробега принимает вид
. В результате более точное выражение для длины свободного пробега принимает вид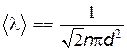 .
.
 2015-02-04
2015-02-04 335
335







