В явлениях переноса каждая молекула переносит от слоя к слою некоторую физическую микроскопическую величину a: среднюю энергию движения в явлении теплопроводности – 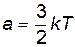 ; массу в явлении диффузии – a=m0; импульс направленного движения в явлении вязкости – a=mu (см. табл. 8.1)
; массу в явлении диффузии – a=m0; импульс направленного движения в явлении вязкости – a=mu (см. табл. 8.1)
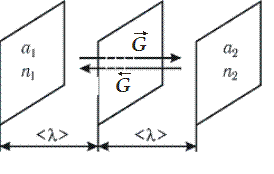 Рис. 8.11. Рис. 8.11. |
Задача молекулярно-кинетической теории состоит в установлении связей между макроскопическими характеристиками явлений переноса dG и микрохарактеристиками a. Для установления этой связи вычислим поток физической величины a через площадку S. На расстоянии, равном длине свободного пробега 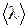 , слева и справа расположим еще две такие же площадки (рис. 8.11). В месте расположения этих площадок значения физических величин a1 и a2, переносимых молекулами, различны. В общем случае различны также скорости хаотического движения молекул (
, слева и справа расположим еще две такие же площадки (рис. 8.11). В месте расположения этих площадок значения физических величин a1 и a2, переносимых молекулами, различны. В общем случае различны также скорости хаотического движения молекул (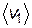 и
и 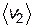 ), а в случае явления диффузии – концентрация примесных молекул (n1 и n2). Однако, поскольку скорость хаотического движения молекулы меняется с температурой очень медленно, (
), а в случае явления диффузии – концентрация примесных молекул (n1 и n2). Однако, поскольку скорость хаотического движения молекулы меняется с температурой очень медленно, (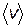 ~
~ 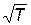 см. формулу (8.18)), то можно считать, что
см. формулу (8.18)), то можно считать, что 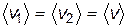 .
.
|
|
|
Поскольку расстояние между площадками равно длине свободного пробега, то молекулы проходят его без столкновений. Очевидно, что поток физической величины a можно найти, умножив a на число молекул dN, пересекающих центральную площадку за время dt:
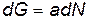 , , |
где dN определяется формулой (8.4).
Поток слева направо: 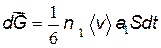 ;
;
поток справа налево: 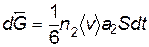 .
.
Суммарный поток определяется разностью
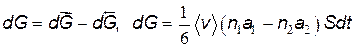 . . | (8.35) |
Формула (8.35) – основная при рассмотрении конкретных явлений переноса.
1. Явление теплопроводности. В этом случае (см. табл. 8.1)
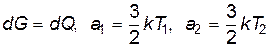 , , |
поэтому из формулы (8.35) следует
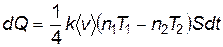 . . |
В явлении теплопроводности основную роль играет перепад температур, поэтому можно считать, что значения концентраций n1 и n2 одинаковы: n1=n2=n. В связи с этим
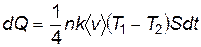 . . | (8.36) |
Выразим разность температур T1-T2 через ее градиент:
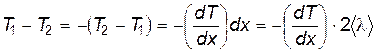 . . | (8.37) |
где вместо dx взято расстояние между крайними площадками, равное 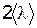 .
.
С учетом (8.37) выражение (8.36) принимает вид
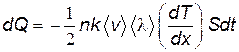  . . | (8.38) |
Полученное уравнение совпадает с уравнением теплопроводности (8.31). Из сопоставления этих уравнений находим коэффициент теплопроводности
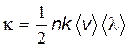 . . | (8.39) |
2. Явление диффузии. Для основного газа поток dG=0, поскольку концентрация этого газа распределена по объему равномерно: n1=n2=n. Поэтому в выражении (8.35) мы должны учесть лишь поток, вызванный молекулами примеси. Положив в этом случае a1=a2=m0 и заменив концентрации основного газа n1 и n2 на концентрации примеси n10 и n20, из формулы (8.35) получим
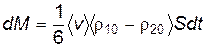 . . | (8.40) |
где r10-r20=n10m0-n20m0 – разность плотностей примесного газа, как и в предыдущем случае, можно выразить через градиент
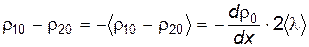 . . | (8.41) |
Подставим (8.41) в (8.40):
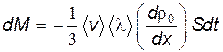 . . |
Полученное уравнение совпадает с уравнением диффузии (8.32). Из сопоставления этих уравнений находим коэффициент диффузии
|
|
|
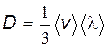 . . | (8.42) |
3. Явление вязкости. В этом случае (табл. 8.1) dG=dK, a1=mu1, a2=mu2, поэтому уравнение (8.35) принимает вид
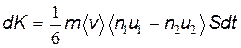 . . | (8.43) |
В явлении вязкости основную роль играет перепад скорости направленного движения, поэтому n1=n2=n и уравнение (8.43) принимает вид
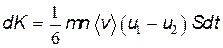 . . |
Снова, как и в явлении теплопроводности, выразим разность через соответствующий градиент:
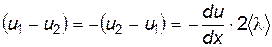 . . |
Тогда
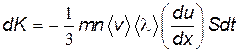 . . |
Полученное уравнение совпадает с уравнением вязкости (8.33). Из сопоставления этих уравнений можно найти коэффициент вязкости
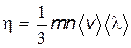 . . |
 2015-02-04
2015-02-04 6816
6816
