Пример № 1

Определим в R алгебраические операци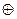и и следующим образом:

а 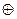b = a + b + 1,

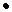a b = a + b + a b,

где «+» и «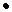» в правых частях этих равенств являются обычным сложением и умножением чисел.

Докажем, например, что в этом примере является ассоциативной.

Доказательство.

Мы должны доказать, что

(a b) с = a (b c).

Имеем

(a b) c = (a + b + ab) c = (a + b + ab) + c + (a + b + ab)с = a + b + c + ab + ac + bc + abc = a + (b + c) + a(b + c + bc) + bc = a + (b + c + bc) + a(b + c + bc) = a (b + c + bc) = a (b c).

Можно так же показать, что операция 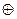является ассоциативной.

Если в множестве М, в котором определена алгебраическая операция, имеется элемент е, такой, что для всякого

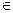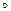а М е а = а 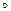е = а,

то говорим, что элемент е является единичным элементом операции .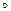

Если рассматривать какое – либо из множеств N, Z, Q, R, C со сложением, то единичным элементом будет число 0. В тех же множествах, рассматриваемых с умножением в качестве алгебраической операции, единичным элементом является 1.

Во множестве всех четных чисел с умножением в качестве алгебраической операции нет единичного элемента. В данном множестве М с данной алгебраической операцией. Не может быть больше чем один единичный элемент. В самом деле, если бы е и е' были бы единичными элементами операции 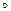, то было бы

е 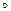е' = е' и е 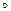е' = е,

откуда е = е'.