2015-02-14
256
Полугруппа G с единицей е называется группой, если для каждого ее элемента а существует такой элемент а'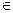 
G, что
а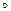 
а' = а' 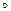а = е. (1)
Будем с этого момента алгебраическую операцию в группе называть умножением и обозначать символом обычного умножения, ее результат будем называть произведением. Элемент а' из (1) назовем обратным к а и обозначим символом а-1. Таким образом (1) запишется так:
а 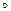а-1 = а-1 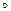а = е. (1')
Определение 2.
Группа – это множество замкнутое относительно одной ассоциативной алгебраической операции, содержащее единичный элемент и такой, что для каждого ее элемента а существует обратный элемент, который удовлетворяет равенству (1').
