Множество Z можно разбить на классы чисел сравнимых между собой по модулю m и называемых классами вычетов по модулю m. Каждый класс вычетов имеет вид
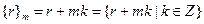 ,
,
так что
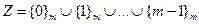 .
.
Каждым двум классам 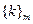 и
и 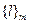 независимо от выбора в них представителей k, l можно сопоставить классы, являющиеся их суммой или произведением, то есть на множестве
независимо от выбора в них представителей k, l можно сопоставить классы, являющиеся их суммой или произведением, то есть на множестве 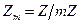 классов вычетов по модулю m однозначным образом индуцируются операции
классов вычетов по модулю m однозначным образом индуцируются операции 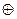 и
и 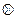 :
:
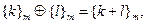
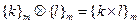
Так как определения этих операций сводятся к соответствующим операциям над числами из классов вычетов, то есть над элементами из Z, то { Zm, 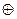 ,
, 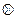 } будет так же коммутативным кольцом с единицей
} будет так же коммутативным кольцом с единицей 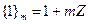 . Оно называется кольцом классов вычетов по модулю m. Итак мы показали, что конечные кольца существуют. Приведем три примера, указывая отдельно таблицы сложения и умножения:
. Оно называется кольцом классов вычетов по модулю m. Итак мы показали, что конечные кольца существуют. Приведем три примера, указывая отдельно таблицы сложения и умножения:
| + | ||
| ∙ | ||
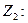
| + | |||
| ∙ | |||
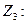
| + | ||||
| ∙ | ||||
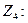
 2015-02-14
2015-02-14 423
423








