Определение.
Пусть К – не пустое множество, на котором заданы две бинарные алгебраические операции «+» (сложение) и «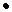 » (умножение), удовлетворяющие следующим условиям:
» (умножение), удовлетворяющие следующим условиям:
1). (К, +) – абелева группа;
2). (К, 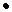 ) – полугруппа;
) – полугруппа;
3). операции (+) и (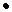 ) связаны дистрибутивными законами (другими словами, умножение дистрибутивно по сложению).
) связаны дистрибутивными законами (другими словами, умножение дистрибутивно по сложению).
(a+b)c=ac+bc, c(a+b)=ca+cb 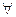 a,b,c
a,b,c 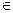 К.
К.
Тогда (К,+, 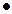 ) называется кольцом. Структура (К, +) называется аддитивной группой кольца, (К,
) называется кольцом. Структура (К, +) называется аддитивной группой кольца, (К, 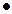 ) – его мультипликативной полугруппой. Если (К,
) – его мультипликативной полугруппой. Если (К, 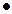 ) – моноид (полугруппа с 1), то говорят, что (К,+,
) – моноид (полугруппа с 1), то говорят, что (К,+, 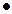 ) - кольцо с 1.
) - кольцо с 1.
Единичный элемент кольца принято обозначать 1. Существование 1 часто вносится в определение кольца. В приложениях и в общей теории колец рассматриваются алгебраические структуры, в которых аксиома 2 либо совсем устраняется, либо заменяется другой, в зависимости от конкретной задачи. В таких случаях говорят о не ассоциативных кольцах. Подмножество L кольца К называется подкольцом, если х,у 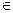 L
L 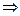 х-у
х-у 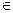 L, ху
L, ху 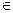 L, то есть если L подгруппа аддитивной группы и подполугруппа мультипликативной полугруппы кольца. Кольцо называется коммутативным, если
L, то есть если L подгруппа аддитивной группы и подполугруппа мультипликативной полугруппы кольца. Кольцо называется коммутативным, если
ху = ух 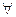 х,у
х,у 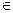 К
К
(в отличие от групп, коммутативное кольцо не принято называть абелевым). 
 2015-02-14
2015-02-14 283
283








