Примеры колец

1. (Z,+, 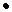) – кольцо целых чисел с обычными операциями + и 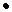). Множество mZ целых чисел делящихся на m, будет в Z подкольцом (без 1 при m >1).

Кольцами с 1 являются Q и R, причем естественные включения 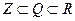определяют цепочки подколец кольца R.

2. Обозначим 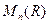(или 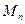) множество всех квадратных матриц (а_ij) порядка n с вещественными коэффициентами а_ij. Очевидно, что 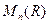- кольцо с единицей Е (Е– единичная матрица). Оно называется полным матричным кольцом над R. Так как при n>1 матрицы, как правило, неперестановочны, то 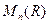– некоммутативное кольцо. Оно содержит в качестве подколец кольца 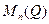и 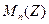квадратных матриц того же порядка над Q и Z соответственно.