Пусть 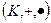 и (К',
и (К', 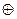 ,
,  )– кольца. Отображение f:К
)– кольца. Отображение f:К 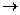 К' называется гомоморфизмом, если оно сохраняет все операции, то есть если
К' называется гомоморфизмом, если оно сохраняет все операции, то есть если
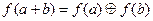 ,
, 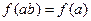
 f(b).
f(b).
При этом, конечно, f(0)=0'и f (na) = nf (a), n 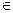 Z.
Z.
Ядром гомоморфизма f называется множество
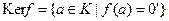 .
.
Ясно, что Кer f - подкольцо в К. Как и в случае групп гомоморфизм f: К в К' называется мономорфизмом, если Кer f = 0. Эпиморфизмом, если образ совпадает сК', то есть
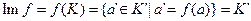 .
.
Изоморфизмом, если отображение f мономорфно и эпиморфно.
Факт изоморфизма колец кратко записывают в виде 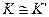 . Отображение
. Отображение 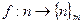 является эпиморфизмом Z в Zm с ядром Кer f=mZ. Если рассматривать только кольца с 1, то в определение гомоморфизма f: К
является эпиморфизмом Z в Zm с ядром Кer f=mZ. Если рассматривать только кольца с 1, то в определение гомоморфизма f: К 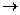 К', целесообразно ввести условие
К', целесообразно ввести условие 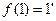 .
.
 2015-02-14
2015-02-14 280
280








