Нетривиальное коммутативное кольцо К с единицей является целостным тогда и только тогда, когда в нем выполнен закон сокращения
ab = ac, a 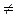 0, b
0, b 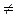 c
c 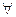 a,b,c
a,b,c 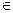 K.
K.
В самом деле, если в К имеет место закон сокращения, то из
аb = 0 = а0 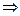 либо а=0, либо а
либо а=0, либо а 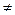 0, но b=0.
0, но b=0.
Обратно: если К область целостности, то
ab = ac, a 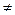 0
0 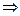 a(b - c) = 0
a(b - c) = 0 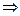 b – c = 0
b – c = 0 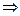 b = c.
b = c.
В кольце К с единицей естественно рассматривать множество обратимых элементов. Элемент а называется обратимым или делителем 1, если существует элемент а-1 для которого 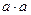 -1 = 1 =
-1 = 1 = 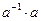 . Точнее следовало бы говорить об элементах обратимых справа или слева (ab=1 или ba=1), но в коммутативных кольцах, а так же в кольцах без делителей нуля, эти понятия совпадают. Действительно, ab=1
. Точнее следовало бы говорить об элементах обратимых справа или слева (ab=1 или ba=1), но в коммутативных кольцах, а так же в кольцах без делителей нуля, эти понятия совпадают. Действительно, ab=1 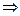 aba=a, откуда
aba=a, откуда
a(ba-1)=0, так как а 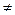 0, то ba-1=0, ba=1.
0, то ba-1=0, ba=1.
Например, в кольце Мn обратимый элемент это в точности матрицы с отличным от нуля определителем.
Обратный элемент a не может быть делителем 0
ab=0 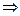 a-1(ab)=0
a-1(ab)=0 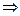 (a-1a)b=0
(a-1a)b=0 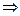
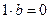
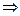 b=0 (аналогично ba=0
b=0 (аналогично ba=0 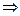 b=0).
b=0).
 2015-02-14
2015-02-14 1072
1072








