В самом деле, так как множество V(К) содержит 1, а 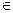 V(К)
V(К) 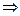 а-1
а-1 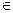 V(К) и ассоциативность по умножению в К выполнена, то надо только убедиться в замкнутости множества V(К), то есть проверить, что произведение аb любых элементов a и b из V(К) будет снова принадлежать V(К), но это очевидно, так как
V(К) и ассоциативность по умножению в К выполнена, то надо только убедиться в замкнутости множества V(К), то есть проверить, что произведение аb любых элементов a и b из V(К) будет снова принадлежать V(К), но это очевидно, так как 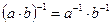
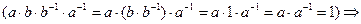 аb - обратим.
аb - обратим.
Легко видеть, что 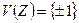 - циклическая группа порядка 2.
- циклическая группа порядка 2.
Мы получили интересный класс колец, так называемое кольцо с делением или тела. Заметив, в определении кольца аксиому К2) на существенно более сильные условия К2') относительно операции умножения множество К\ 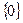 является группой. Кольцо с делением всегда без делителей нуля и каждый не нулевой элемент в нем обратим.
является группой. Кольцо с делением всегда без делителей нуля и каждый не нулевой элемент в нем обратим.
Операции «+» и «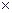 » становятся почти полностью симметричными в коммутативном кольце с делением, которое называется полем.
» становятся почти полностью симметричными в коммутативном кольце с делением, которое называется полем.
 2015-02-14
2015-02-14 259
259








