2015-02-14
406
Поле Р – это коммутативное кольцо с единицей (1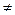 
0) в котором каждый элемент обратим а 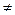0.
Группа Р*=V(Р) называется мультипликативной группой поля. Поле представляет собой гибрид двух абелевых групп: аддитивной и мультипликативной, связанных законом дистрибутивности. Теперь уже одним в виду коммутативности. Подполем F поля Р называется подкольцо в Р. Само являющееся полем, например: поле рациональных чисел Q- подполем поля вещественных чисел R. В случае F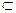 
P говорят также, что поле Р является расширением своего подполя F, из определения подполя следует, что нуль и единица поля Р будут содержаться в F и служить для F нулем и единицей. Говорят, что расширение F1 поля F получено присоединением к F элемента а и отражают это записью f1=f(a). Аналогично можно говорить о подполе F1=F(a1,…,an) поля Р, полученном присоединением к F элемента а и отражают это записью F1=F(a). Аналогично можно говорить о подполе F1=F(a1,…,an) поле Р, полученном присоединением к F n элементов (a1,…,an). Проверка показывает, что Q(
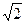) совпадает с множеством чисел а+b 
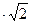, где а,b 
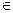Q так как (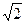)2=2 и
.
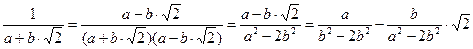При a+b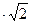 
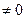то же самое относится к 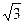Q(
),Q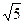 
и так далее.
