Полагая, что длина изготавливаемой детали есть нормально распределённая случайная величина с математическим ожиданием 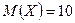 и средним квадратическим отклонением
и средним квадратическим отклонением 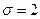 , найти вероятность того, что длина наугад взятой детализаключена в интервале
, найти вероятность того, что длина наугад взятой детализаключена в интервале 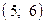 .
.
В каких границах (симметричных относительно 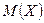 ) будет заключена длина наугад взятой деталис вероятностью 0,95?
) будет заключена длина наугад взятой деталис вероятностью 0,95?
Решение.
Пусть случайная величина 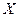 – длина изготавливаемой детали.
– длина изготавливаемой детали.
1) Найдём вероятность того, что 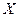 примет значение из интервала
примет значение из интервала 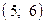 .
.
Вероятность попадания в заданный интервал 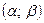 нормально распределённой случайной величины
нормально распределённой случайной величины 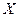 вычисляется по формуле:
вычисляется по формуле: 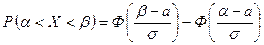 , где
, где
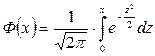 – функция Лапласа,
– функция Лапласа,
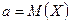 – математическое ожидание случайной величины
– математическое ожидание случайной величины 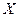 ;
;
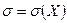 – среднее квадратическое отклонение.
– среднее квадратическое отклонение.
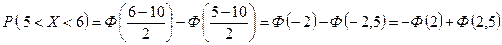 .
.
По таблице значений функции Лапласа находим: 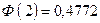 ,
, 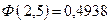 .
.
Значит вероятность того, что 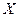 примет значение из интервала
примет значение из интервала 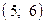 :
:
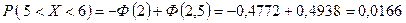 .
.
2) Вероятность заданного отклонения нормально распределённой случайной величины 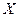
вычисляется по формуле: 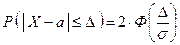 , где
, где 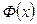 – функция Лапласа,
– функция Лапласа,
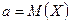 – математическое ожидание случайной величины
– математическое ожидание случайной величины 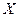 ;
;
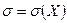 – среднее квадратическое отклонение.
– среднее квадратическое отклонение.
Определим, в каких границах (симметричных относительно 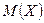 ) будет заключена длина наугад взятой деталис вероятностью 0,95.
) будет заключена длина наугад взятой деталис вероятностью 0,95.
Для этого из равенства 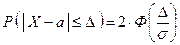 , то есть
, то есть 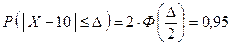 выразим
выразим 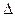 :
:
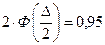 ;
; 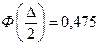 , откуда по таблице значений функции Лапласа
, откуда по таблице значений функции Лапласа
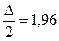 ;
; 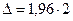 ;
; 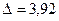 .
.
Таким образом, точность длины (т.е. отклонение от её среднего значения), которую можно гарантировать с вероятностью 0,95, составляет 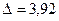 . Следовательно, длина наугад взятой деталис вероятностью 0,95 будет заключена в следующих границах (симметричных относительно
. Следовательно, длина наугад взятой деталис вероятностью 0,95 будет заключена в следующих границах (симметричных относительно 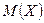 ):
): 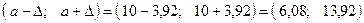
Ответ: 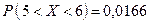 ; длина наугад взятой деталис вероятностью 0,95 будет заключена в интервале
; длина наугад взятой деталис вероятностью 0,95 будет заключена в интервале 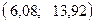 .
.
 2015-02-14
2015-02-14 2170
2170
