Одна из случайных величин 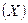 задана законом распределения
задана законом распределения
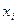 | |||
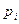 | 0,2 | 0,3 | 0,5 |
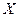 :,
:,
а другая 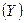 имеет биномиальное распределение с параметрами
имеет биномиальное распределение с параметрами 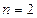 ,
, 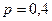 . Составить закон распределения их разности. Найти математическое ожидание и дисперсию этой случайной величины.
. Составить закон распределения их разности. Найти математическое ожидание и дисперсию этой случайной величины.
Решение.
Дискретная случайная величина 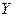 имеет биномиальный закон распределения с параметрами
имеет биномиальный закон распределения с параметрами 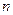 и
и 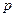 , если она принимает значения
, если она принимает значения 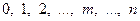 с вероятностями
с вероятностями 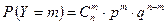 , где
, где 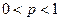 ,
, 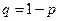 ,
, 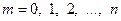 ;
;
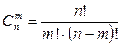 – число сочетаний из
– число сочетаний из 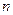 элементов по
элементов по 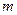 .
.
Биномиальный закон распределения с параметрами 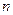 и
и 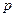 представляет собой закон распределения числа
представляет собой закон распределения числа 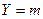 наступлений события
наступлений события 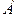 в
в 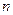 независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью
независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью 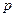 .
.
Ряд распределения биномиального закона имеет вид:
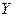 | … | 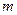 | … | 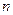 | |||
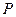 | 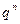 | 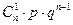 | 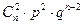 | … | 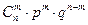 | … | 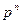 |
Математическое ожидание случайной величины 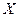 , распределённой по биномиальному закону,
, распределённой по биномиальному закону, 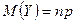 , а её дисперсия
, а её дисперсия 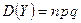 .
.
В нашем случае биномиальный закон распределения имеет параметры 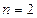 и
и 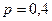 , то есть случайная величина
, то есть случайная величина 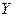 принимает значения
принимает значения 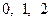 с вероятностями
с вероятностями 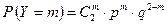 , где
, где 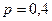 ,
, 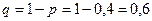 ,
, 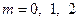 .
.
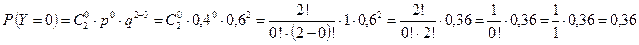 ;
;
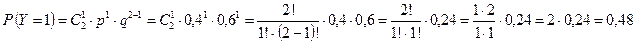 ;
;
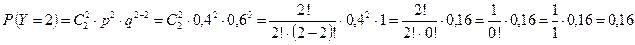 .
.
Таким образом, заданный закон биномиального распределения случайной величины 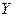 имеет вид:
имеет вид:
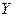 | |||
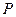 | 0,36 | 0,48 | 0,16 |
Найдём закон распределения случайной величины 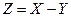 .
.
Разностью случайных величин 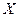 и
и 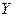 называется случайная величина, которая принимает все возможные значения вида
называется случайная величина, которая принимает все возможные значения вида 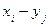 , где
, где 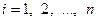 ,
, 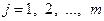 , с вероятностями
, с вероятностями 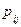 того, что случайная величина
того, что случайная величина 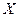 примет значение
примет значение 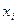 , а
, а 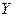 – значение
– значение 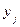 :
: 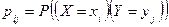 . Если случайные величины
. Если случайные величины 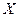 и
и 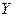 независимы, то по теореме умножения вероятностей независимых событий
независимы, то по теореме умножения вероятностей независимых событий 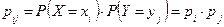 .
.
Для удобства нахождения всех значений разности 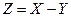 и их вероятностей составим вспомогательную таблицу, в каждой клетке которой поместим в левом верхнем углу значения разности
и их вероятностей составим вспомогательную таблицу, в каждой клетке которой поместим в левом верхнем углу значения разности 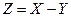 , а в правом нижнем углу – вероятности этих значений, полученные в результате перемножения вероятностей соответствующих значений случайных величин
, а в правом нижнем углу – вероятности этих значений, полученные в результате перемножения вероятностей соответствующих значений случайных величин 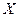 и
и 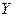 (в нашем случае случайные величины
(в нашем случае случайные величины 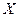 и
и 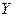 независимы).
независимы).
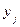 | ||||
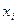 | 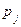 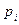 | 0,36 | 0,48 | 0,16 |
| 0,2 | 0,072 | 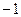 0,096 0,096 | 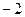 0,032 0,032 | |
| 0,3 | 0,108 | 0,144 | 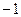 0,048 0,048 | |
| 0,5 | 0,18 | 0,24 | 0,08 |
Так как среди 9 значений 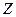 имеются повторяющиеся, то соответствующие вероятности их складываем по теореме сложения вероятностей:
имеются повторяющиеся, то соответствующие вероятности их складываем по теореме сложения вероятностей:
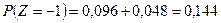 ;
; 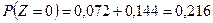 ;
;
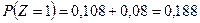 .
.
Таким образом, закон распределения случайной величины 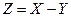 имеет вид:
имеет вид:
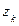 | 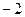 | 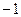 | ||||
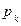 | 0,032 | 0,144 | 0,216 | 0,188 | 0,24 | 0,18 |
Убеждаемся в том, что сумма вероятностей всех возможных исходов равна 1.
Действительно, 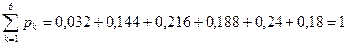 .
.
Вычислим математическое ожидание и дисперсию случайной величины 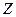 .
.
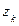 | 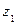 | 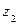 | … | 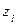 |
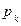 | 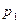 | 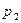 | … | 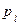 |
Математическое ожидание дискретной случайной величины 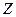 , закон распределения которой имеет вид, вычисляется по формуле
, закон распределения которой имеет вид, вычисляется по формуле 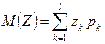 .
.
В нашем случае 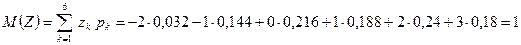 .
.
Дисперсия характеризует степень изменчивости значений случайной величины относительно её математического ожидания. Дисперсию дискретной случайной величины 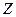 определим по формуле:
определим по формуле:
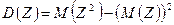 , где
, где 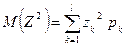 .
.
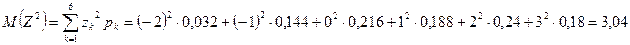 ,
,
значит 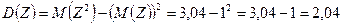 .
.
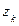 | 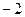 | 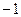 | ||||
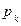 | 0,032 | 0,144 | 0,216 | 0,188 | 0,24 | 0,18 |
Ответ:; 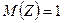 ;
; 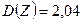 .
.
 2015-02-14
2015-02-14 3957
3957
