Завод «Пино» (г. Новороссийск) отправил в Москву 2000 бутылок вина «Каберне». Вероятность того, что в пути может разбиться бутылка, равна 0,002. Какова вероятность того, что в пути будет разбито не более пяти бутылок?
Решение.
Здесь мы имеем дело с независимыми испытаниями, каждое из которых заключается в перевозке бутылки вина «Каберне» с завода «Пино» в Москву. Число испытаний в нашем случае  .
.
Пусть 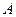 – событие, которое заключается в том, что в пути бутылка вина разбилась.
– событие, которое заключается в том, что в пути бутылка вина разбилась.
Вероятность того, что в пути будет разбито не более пяти бутылок равна 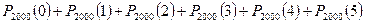 .
.
Вычислить искомую вероятность по формуле Бернулли 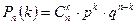 затруднительно из-за громоздкости вычислений. Искомую вероятность можно вычислить, используя асимптотическую (приближённую) формулу Пуассона.
затруднительно из-за громоздкости вычислений. Искомую вероятность можно вычислить, используя асимптотическую (приближённую) формулу Пуассона.
Итак, воспользуемся теоремой Пуассона:
если вероятность 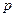 наступления события
наступления события 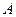 в каждом испытании постоянна и мала
в каждом испытании постоянна и мала 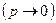 , число испытаний
, число испытаний 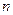 – велико
– велико 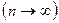 и число
и число 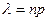 – незначительно
– незначительно 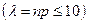 , то вероятность
, то вероятность 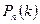 того, что событие
того, что событие 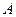 появится
появится 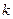 раз в
раз в 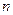 независимых испытаниях вычисляется по приближённой формуле
независимых испытаниях вычисляется по приближённой формуле 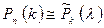 , где
, где 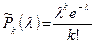 – функция Пуассона.
– функция Пуассона.
В нашем случае вероятность появления события 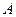
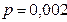 постоянна и мала, число независимых испытаний
постоянна и мала, число независимых испытаний  велико, число
велико, число 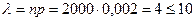 .
.
Значит вероятность появления события 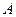 не более 5 раз в 2000 испытаниях:
не более 5 раз в 2000 испытаниях:
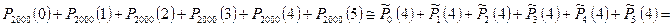
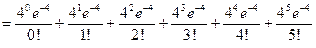 .
.
По таблице значений функции Пуассона находим:
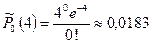 ;
; 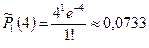 ;
; 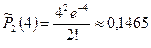 ;
;
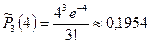 ;
; 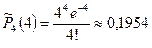 ;
; 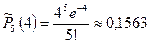 .
.
Следовательно, вероятность того, что в пути будет разбито не более пяти бутылок равна
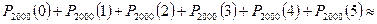
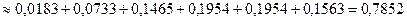 .
.
Ответ: 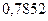 .
.
 2015-02-14
2015-02-14 2113
2113








