Вычисление элементов матриц грузовых перемещений

Каждый элемент 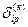матриц 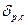и 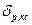канонических уравнений (1.5) и (1.6) физически представляют собой перемещение по направлению i-го неизвестного от воздействия силы 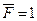при ее расположении в любом из заданных сечений «к» верхнего ригеля рамы. Эпюра моментов 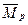, построенная в основной системе для случая произвольного положения силы 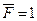в пролете, показана на рис.10,а.

Используя группировки силы 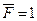на симметричное и кососимметричное парные воздействия (рис.10,б,в) построим две грузовые эпюры моментов 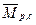и 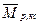, сумма ординат которых соответствует исходному воздействию. Вычислять перемещения с помощью этих эпюр значительно проще, так как первая дает отличный от нуля результат только при сопряжении с соответствующими эпюрами от симметричных неизвестных, а вторая – с эпюрами от кососимметричных неизвестных.

Сопрягая эпюру 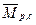с эпюрой 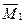(симметричные относительно вертикальной оси участки этих эпюр показаны на рис.11,а), получим аналитическое выражение для элементов вектора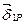

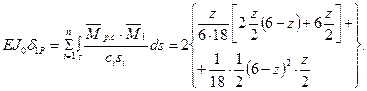
После соответствующих преобразований получим

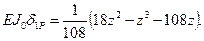(3.1)

Аналогично, сопрягая эпюры 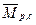и 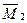, запишем

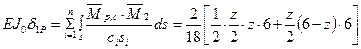
или 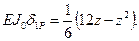(3.2)

Для сопряжения грузовой эпюры 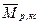по правилу Верещагина с единичными эпюрам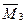и и 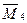, предварительно найдем положение центра тяжести треугольника (рис.11,б), который соответствует левой (относительно оси симметрии) части грузовой эпюры моментов.

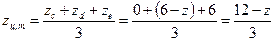
Тогда ординаты на эпюрах 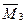и 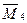под центром тяжести грузовой эпюры моментов:

, .

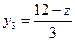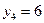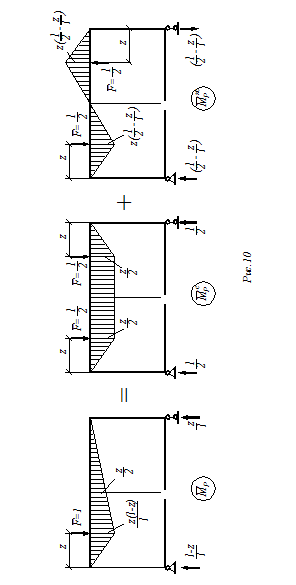
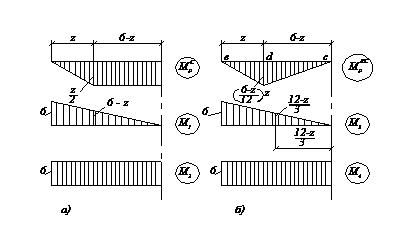
Рис. 11

Перемножение, указанных выше эпюр приводит к следующим результатам:

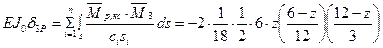
или

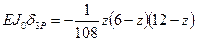; (3.3)

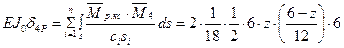
или

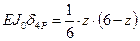. (3.4)

Полученные аналитические выражения (3.1) и (3.4) позволяют вычислять элементы матриц 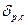и 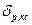при изменении положения силы F=1 в следующих пределах: 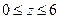, т.е. до оси симметрии рамы.