Построение линий влияния неизвестных

Аналитические выражения для вычисления ординат линий влияния симметричных неизвестных получим, раскрывая следующие матричные записи решения систем канонических уравнений (1.5) и (1.6):

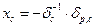; (3.5)

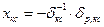; (3.6)

Подставив обратную матрицу 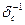(1.9) и вектор 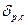в виде зависимостей (3.1) и (3.2), можем записать

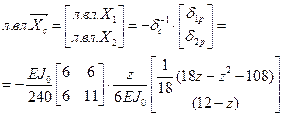
Перемножая элементы столбца матрицы 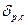на численные значения элементов первой строки матрицы 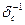с учетом постоянного коэффициента перед ней, получим (после сложения результатов и алгебраических преобразований) уравнение линии влияния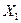

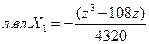. (3.7)

Аналогично, путем перемножения того же столбца на элементы второй строки получим уравнение линии влияния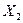

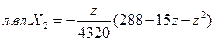. (3.8)

Линии влияния симметричных неизвестных показаны рис.12,а,б. Ординаты линий влияния вычислены с шагом через один метр в сечениях ригеля с номерами от 0 до 6. С учетом симметрии ординаты этих линий влияния на правой части ригеля имеют те же значения, как по величине, так и по знаку.

Раскрывая матричную запись (3.6) подстановкой матрицы 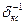(1.10) и вектора 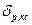в виде зависимостей (3.3) и (3.4), в общем виде, запишем:

.

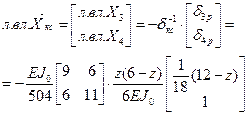Осуществив операции перемножения столбца 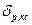на соответствующие строки матрицы 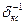, получим следующие уравнения линий влияния кососимметричных неизвестных:

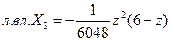; (3.9)

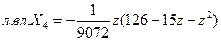. (3.10)

Вид линий влияния кососимметричных неизвестных показан на рис.12,в,г. В сечениях ригеля рамы с номерами от 0’ до 5’ ординаты этих линий влияния имеют обратный знак.

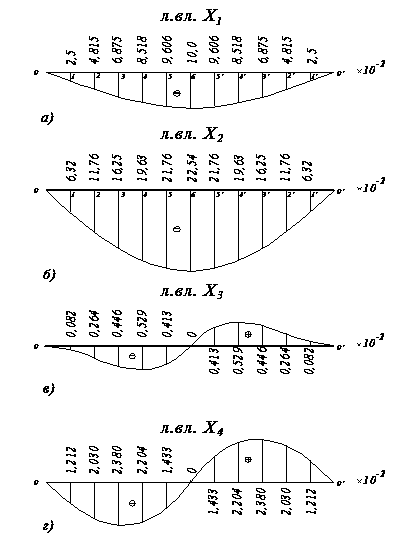
Рис.12