В этом случае уравнение Шредингера имеет вид:
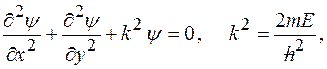 (1)
(1)
в пределах ямы 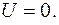
На сторонах ямы  функция должна обращаться в нуль, поскольку является непрерывной (за пределами ямы
функция должна обращаться в нуль, поскольку является непрерывной (за пределами ямы  ). Поэтому
). Поэтому 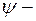 функцию внутри ямы удобнее искать в виде произведения синусов
функцию внутри ямы удобнее искать в виде произведения синусов
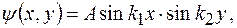 (2)
(2)
так как на двух сторонах 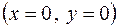 автоматически
автоматически 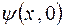 и
и 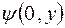 равны нулю.
равны нулю.
Возможные значения 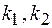 найдем из условия обращения
найдем из условия обращения 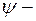 функции в нуль на противоположных сторонах ямы:
функции в нуль на противоположных сторонах ямы:
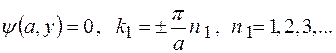
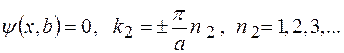 (3)
(3)
После подстановки (3) в уравнение (2) получим 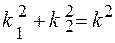 , и
, и 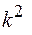 в (1) получим:
в (1) получим:
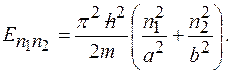 (4)
(4)
Постоянную 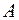 в (2) находим из условия нормировки
в (2) находим из условия нормировки
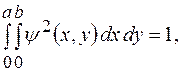
Откуда следует, что 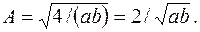 Следовательно, нормированная
Следовательно, нормированная 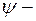 функция будет иметь вид:
функция будет иметь вид:
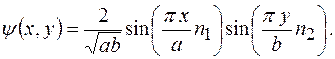
Ответ: 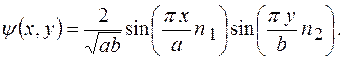
 2015-02-14
2015-02-14 522
522








