Задачи для самостоятельного решения. 1. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной находится в возбужденном состоянии n=2

1. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 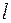находится в возбужденном состоянии n =2. Определить, в каких точках интервала (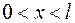) плотность вероятности нахождения частиц максимальна.

2. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 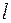находится в возбужденном состоянии n =2. Найти вероятность нахождения частицы в последней трети ящика.

3. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 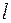находится в основном состоянии. Найти вероятность нахождения частицы в области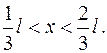

4. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 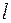в основном состоянии. В каких точках интервала (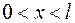) плотность вероятности нахождения частиц максимальна.

5. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 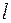находится в возбужденном состоянии n =2. Определить, в каких точках интервала (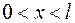) плотность вероятности нахождения частиц минимальна.

6. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 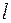, в основном состоянии. Определить среднее значение координаты электрона.

7. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 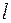находится в возбужденном состоянии с n =2. Определить среднее значение координаты электрона.

8. Электрон находится в потенциальном ящике шириной 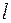. В каких точках в интервале 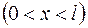плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить плотность вероятности для этих точек. Решение пояснить графически.

9. Частица в потенциальном ящике находится в основном состоянии. Какова вероятность 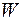нахождения частицы: 1) в средней трети ящика; 2) в крайней трети ящика?

10. В одномерном потенциальном ящике шириной 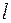находится электрон. Вычислить вероятность 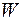нахождения электрона на первом энергетическом уровне в интервале 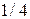, равноудаленном от стенок ящика.

11. Частица в потенциальном ящике шириной 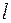находится в низшем возбужденном состоянии. Определить вероятность 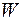нахождения частицы в интервале 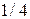, равноудаленном от стенок ящика.

12. Электрон находится в одномерной прямоугольной «потенциальной яму» шириной 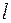с бесконечно высокими «стенками». Определить вероятность 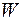обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии ( 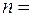2). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.

13. Прямоугольный потенциальный барьер имеет ширину 0.1 нм. Определить в эВ разность энергий 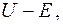при которой вероятность прохождения электрона сквозь барьер составит 0,99.

14. Вычислить отношение вероятностей 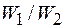нахождения электрона на первом и втором энергетических уровнях в интервале 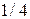, равноудаленном от стенок одномерной потенциальной ямы шириной .

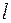15. Показать, что собственные функци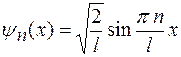и и 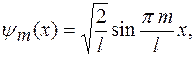описывающие состояние частицы в потенциальном ящике, удовлетворяют условию ортогональности, т.е.

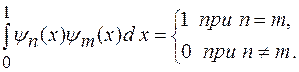
16. Используя выражение энергии 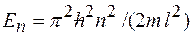частицы, находящейся в потенциальном ящике, получить приближенное значение энергии: 1) гармонического осциллятора; 2) водородоподобного атома. Сравнить полученные результаты с истинными значениями энергий.

17. Считая, что нуклоны в ядре находятся в трехмерном потенциальном ящике кубической формы с линейными размерами 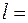10фм, оценить низший энергетический уровень нуклонов в ядре.

18. Определить из условия нормировки коэффициент 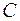собственной 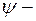функции 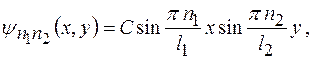описывающей состояние электрона в двумерном бесконечно глубоком потенциальном ящике со сторонам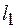и и .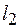

19. Электрон находится в основном состоянии в двумерном квадратном бесконечно глубоком потенциальном ящике со сторонами 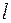. Определить вероятность 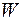нахождения электрона в области, ограниченной квадратом, который равноудален от стенок ящика и площадь которого составляет 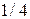площади ящика.

20. Определить из условия нормировки коэффициент собственной 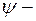функции 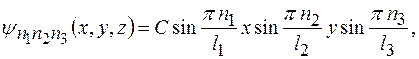описывающей состояние электрона в трехмерном потенциальном бесконечно глубоком ящике со сторонами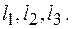

21. Зная отношение амплитуд вероятности 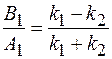для волны, отраженной от барьера, и 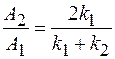для проходящей волны, найти выражение для коэффициента отражения 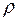и коэффициента прохождения .

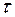22. Считая выражение для коэффициента отражения 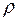от потенциального барьера и коэффициента прохождения 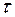известными, показать, что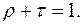

23. Протон с энергией 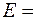1 МэВ изменил при прохождении потенциального барьера дебройлевскую длину волны на 1%. Определить высоту 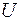потенциального барьера.

24. На пути электрона с дебройлевской длиной волны 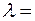0,1 нм находится потенциальный барьер высотой 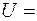120 эВ. Определить длину волны де Бройля после прохождения барьера.

25. Определить показатель преломления 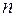волн де Бройля при прохождении частицей потенциального барьера с коэффициентом отражения 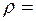0,5.

26. Электрон с энергией 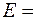100 эВ попадает на потенциальный барьер высотой 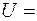64 эВ. Определить вероятность 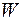того, что электрон отразится от барьера.

27. Кинетическая энергия 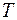электрона в два раза превышает высоту 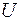потенциального барьера. Определить коэффициент отражения 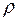и коэффициент прохождения 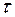электронов на границе барьера.

28. Коэффициент прохождения 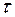электронов через низкий барьер равен коэффициенту отражения 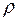. Определить во сколько раз кинетическая энергия 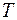электронов больше высоты 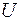потенциального барьера.

29. Коэффициент прохождения 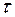протонов через потенциальный барьер равен 0,8. Определить показатель преломления 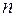волн де Бройля на границе барьера.

30. Вычислить коэффициент прохождения 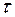электрона с энергией 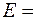100 эВ через потенциальный барьер высотой 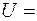99,75 эВ.