Начисление процентов на оставшуюся часть основного долга

В этом случае сумма долга PV уменьшается от платежа к платежу, а проценты I начисляют каждый раз на оставшуюся часть кредита. Основной долг PV выплачивают равными частями. В состав каждого погасительного платежа входят две структурных составляющих: часть, идущая на погашение основного долга PV и часть, идущая на погашение процентов I. Часть 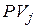, идущая на погашение основного долга, от платежа к платежу не изменяется, и ее величина составляет

.

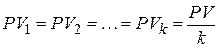(4.12)

В составе первого погасительного платежа проценты 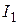начисляют на всю сумму основного долга PV по формуле (2.1), выразив в ней t через период начисления процентов m между платежами: 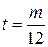. Тогда

.

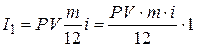(4.13)

Множитель «1» введен в этой формуле для удобства последующего обобщения.

При данном способе начисления процентов сумма очередного погасительного платежа изменяется по отношению к сумме предыдущего. Сумму 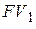первого погасительного платежа определяют по формуле

.

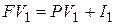(4.14)

После первого погасительного платежа сумма основного долга уменьшится на величину 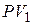и составит 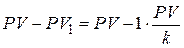(множитель «1» введен для последующего обобщения). На эту часть основного долга происходит начисление процентов 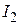в течение следующих m месяцев:

.

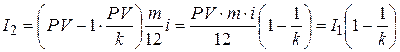(4.15)

Сумму 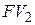второго погасительного платежа определяют по формуле

.

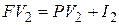После второго погасительного платежа сумма основного долга уменьшится на величину 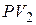и составит 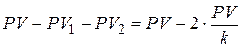. На эту сумму начисляют проценты 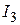в течение следующих m месяцев:

.

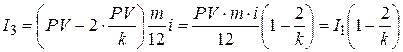(4.16)

Сумму 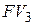третьего погасительного платежа определяют по формуле

.

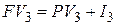Обобщая формулы (4.13), (4.15) и (4.16), получаем для последнего k -го погасительного платежа:

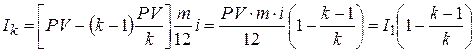	;	(4.17)
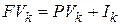	.	(4.18)

Сравнивая формулы (4.13), (4.15), (4.16) и (4.17), нетрудно увидеть, что части платежей, идущие на погашение процентов, уменьшаются в каждом платеже на величину 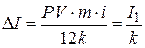. На эту же величину уменьшаются и суммы самих платежей.

Суммарная величина процентных выплат за пользование предоставленным кредитом по всем погасительным платежам с учетом формулы (4.4) составит

.

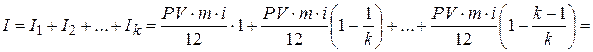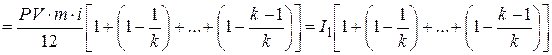В этой формуле сумма в квадратных скобках представляет собой сумму 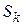конечного числа k членов арифметической прогрессии, в которой 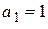, а 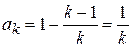. Тогда с учетом формулы (4.3) получим:

.

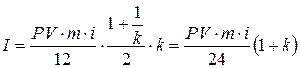(4.19)

Общая сумма кредита FV, включающая основной долг PV и суммарную величину процентных выплат I, с учетом формулы (1.1) составит

.

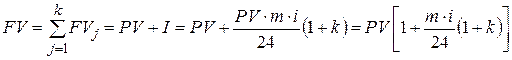(4.20)

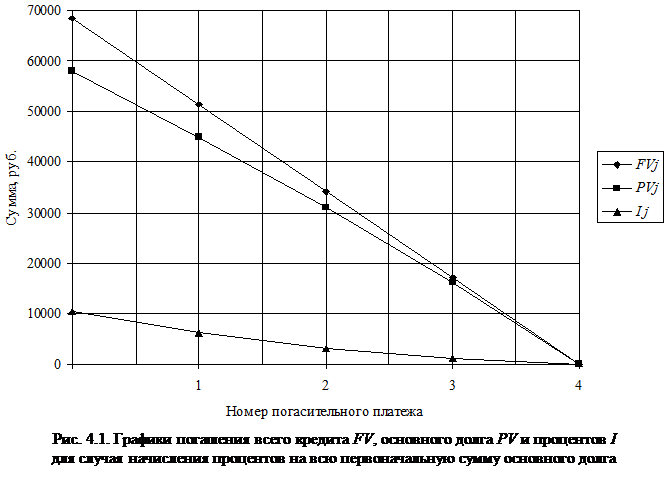
Пример 4.2. В условиях примера 4.1 рассчитать план платежей и построить графики погашения всего кредита, основного долга и процентов, если проценты начисляют каждый раз на оставшуюся непогашенную часть основного долга.