Понятие финансовой эквивалентности

Возникают ситуации, когда участники ФО вынуждены менять суммы и сроки платежей или объединять несколько платежей в один, выполняя их консолидацию, с установлением нового срока погашения консолидированного платежа. В результате любых изменений ни один из участников не должен терпеть убыток. Для этого участники ФО руководствуются принципом финансовой эквивалентности, реализуемым с помощью уравнения эквивалентности, согласно которому сумма заменяемых платежей, приведенных к одному моменту времени (focal date) в прошлом (путем дисконтирования) или в будущем (путем наращения), приравнивается к сумме заменяющего платежа по новому соглашению, приведенного к тому же моменту времени [2, 3]. Например, при замене одного платежа, имеющего будущую стоимость 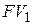и срок погашения 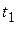, новым платежом, имеющим будущую стоимость 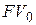и срок погашения 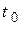, при условии приведения к начальной дате в прошлом путем дисконтирования получим следующее уравнение эквивалентности:

;

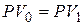(6.1)

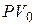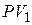где и – приведенные стоимости заменяющего и заменяемого платежей. В зависимости от используемых ставок можно записать следующие частные случаи уравнения эквивалентности:

– при использовании простой процентной ставки [3]

;

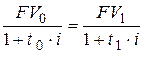(6.2)

– при использовании сложной процентной ставки [2]

;

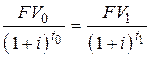(6.3)

– при использовании простой учетной ставки

;

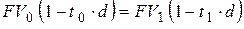(6.4)

– при использовании сложной учетной ставки [2]

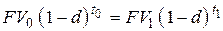(6.5)

При консолидации, т. е. при замене нескольких платежей, имеющих будущие стоимости 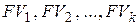и сроки погашения 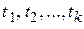, одним новым платежом, имеющим будущую стоимость 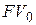и срок погашения 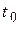, при условии приведения к начальной дате в прошлом путем дисконтирования получим следующее уравнение эквивалентности:

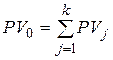(6.6)

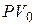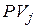где и – приведенные стоимости заменяющего и заменяемых платежей. В зависимости от используемых ставок возможны следующие частные случаи уравнения эквивалентности [2]:

– при использовании простой процентной ставки

;

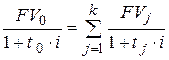(6.7)

– при использовании сложной процентной ставки

;

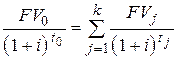(6.8)

– при использовании простой учетной ставки

;

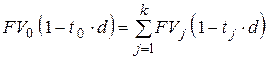(6.9)

– при использовании сложной учетной ставки

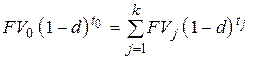(6.10)

Полученные уравнения эквивалентности позволяют в конкретных случаях определять будущую стоимость 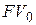заменяющего платежа и срок 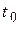его погашения. Если сроки платежей заданы в днях 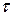, месяцах m или годах n, то полученные уравнения можно преобразовать с учетом формул (1.6)–(1.8).