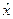
| 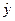
| 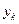
| Модуль
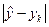
|
В графах табл. 7 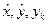 , указываются не только конечные значения, но и исходные для расчета числа.
, указываются не только конечные значения, но и исходные для расчета числа.
2. Мы, в конечном счете, выбираем функцию, 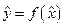 которая бы максимально точно аппроксимировала исследуемый статистический ряд. Однако практика исследований показывает, что крайне редко значение
которая бы максимально точно аппроксимировала исследуемый статистический ряд. Однако практика исследований показывает, что крайне редко значение 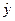 соответствует одному из статистических уi, а попадает в некий интервал i и i+ 1. В этом случае рекомендуется использовать способ линейной интерполяции
соответствует одному из статистических уi, а попадает в некий интервал i и i+ 1. В этом случае рекомендуется использовать способ линейной интерполяции
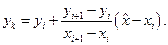
| (62) |
Ориентиром для выбора границ интервалов i и i+ 1 в статистическом ряду является значение 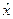 .
.
3. Уравнением регрессии будет то, которое обеспечивает min 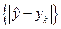 , т.е. минимальное расхождение между статистическим и теоретическим (эмпирическим) распределениями.
, т.е. минимальное расхождение между статистическим и теоретическим (эмпирическим) распределениями.
Выбранное уравнение регрессии указывается в выводе в исследуемых согласно заданию физических величинах.
Определение численных значений коэффициентов уравнения регрессии
Мы рассматриваем относительно простые эмпирические формулы, в которых только два коэффициента – а и b. Для определения их значений используется ряд методов, из которых наиболее часто применяются методы наименьших квадратов и средних.
Метод наименьших квадратов
Требует минимального значения суммы квадратов отклонений 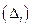 между теоретическими
между теоретическими 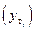 и статическими
и статическими 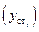 значениями распределений
значениями распределений
 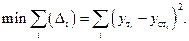
| (63) |
В соответствии с методом наименьших квадратов значения коэффициентов регрессии находятся из решения системы двух уравнений
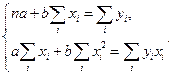
| (64) |
Таким образом, значения коэффициентов a и b определяются по формулам
 , ,
| (65) |
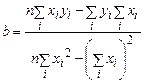 . .
| (66) |
Формулы (64), (65) и (66) справедливы только для линейной (нормальной) зависимости. Для других зависимостей используется прием линиаризаций, т.е. формальное приведение их к виду уравнения прямой линии заменой переменных.
Обратно-пропорциональная зависимость
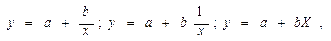
| (67) |
где 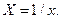
|
Степенная зависимость
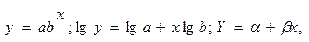
| (68) |
где 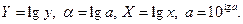
|
Показательная зависимость
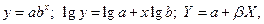
| (69) |
где 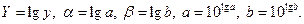
|
Гиперболическая зависимость
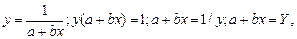
| (70) |
где 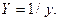
|
Дробно-линейная зависимость
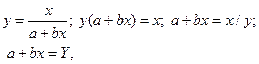
| (71) |
| где Y = x / y. |
Логарифмическая зависимость
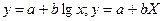
| (72) |
где 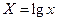 . .
|
Основываясь на вышеизложенном, система уравнений и выражения для определения коэффициентов a и b применительно, например, к показательной зависимости будут иметь вид
 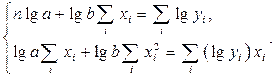
| (73) |

| (74) |
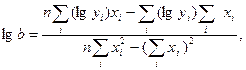
| (75) |
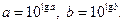
| (76) |
Указание. При расчетах, по вышеприведенным формулам точность в пределах 2–3 знаков после запятой является вполне приемлемой. А применительно к гиперболической и дробно-линейной зависимостям, точность должна быть на уровне 6–7 знаков.
При выполнении конкретного задания студент, применительно к исходным данным, определяет вид уравнения регрессии, выполняет линиаризацию и указывает систему уравнений применительно только к своей зависимости, разрешает систему уравнений и приводит свое уравнение регрессии с численными значениями коэффициентов, например (пример носит условный характер)
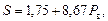 где a = 1,75, b = 8,67. где a = 1,75, b = 8,67.
|
Метод средних требует нулевых отклонений между статическим и теоретическим распределениями и формирование системы линиализированных (нормальных) уравнений по числу имеющихся наблюдений вида
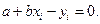
| (77) |
Тогда, например, при n = 4 и показательной зависимости эта система уравнений будет иметь вид
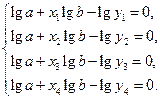
| (78) |
Нетрудно заметить что систему (78) можно решить путем приведения ее к системе двух уравнений почленным сложением отдельно первого и второго, а так же третьего и четвертого уравнений. Система двух уравнений решается методом вычитания, что позволяет получить значение коэффициента b. Коэффициент a определяется из любого уравнения системы (78).
Таким образом, мы имеем два уравнения регрессии, значения коэффициентов которых получены разными методами, и, следовательно, обладают разной степенью адекватности исследуемому явлению.
Выбор адекватного уравнения регрессии производится на базе информации по форме табл. 8.
В табл. 8, под х и у подразумеваются конкретные физические величины из задания.
Размер отклонений определяется по формуле
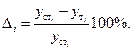
| (79) |
Таблица 8
 2015-02-14
2015-02-14 454
454








