2015-02-14
361
Этот закон наиболее часто используют в практике исследований, т.к. им описывается большинство разнообразных явлений.
Плотность распределения вероятностей (вероятность, приходящаяся на единицу времени, массы, площади и т.д.) выражается формулой
 ,
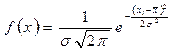| (80) |
где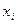 
– значение i –й случайной величины; 
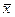– математическое ожидание; 
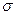– среднее квадратное отклонение; 
, 
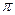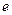– константы.
В расчётах принимать 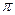=3,1416, 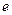=2,7182.
Кривая плотности распределения вероятностей симметрична относительно математического ожидания (рис. 4).
Для нормального закона характерны две особенности:
– малые значения коэффициента вариации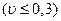 
;
– практически все отклонения от математического ожидания заключены в интервале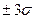 
, а вероятность попадания случайной величины в разные интервалы характеризуется данными:
|
|
|
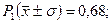
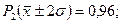
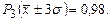
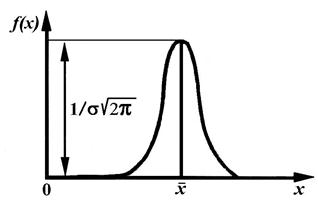
Рис. 4. Вид кривой плотности нормального распределения
Значение максимальной ординаты определяется выражением
 .
|
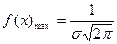Указанные особенности используются для распознавания закона при обработке статистических данных.
|
|
|
