Четность и нечетность функции

Функция 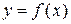называется четной, если для любых и 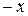, принадлежащих множеству 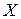, выполняется: .

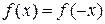График четной функции симметричен относительно оси ординат.

Функция 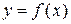называется нечетной, если для любых и 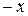, принадлежащих множеству 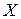, выполняется: .

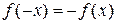График нечетной функции центрально симметричен относительно начала координат.

2) Промежутки возрастания и убывания функции (монотонность).

Функция называется возрастающей на рассматриваемом промежутке, если большему значению аргумента соответствует большее значение функции у(х). Это означает, что если из рассматриваемого промежутка взяты два произвольных аргумента х₁ и х₂, причём х₁ > х₂, то у(х₁) > у(х₂).

Функция называется убывающей на рассматриваемом промежутке, если большему значению аргумента соответствует меньшее значение функции у(х). Это означает, что если из рассматриваемого промежутка взяты два произвольных аргумента х₁ и х₂, причём х₁ < х₂, то у(х₁) < у(х₂).