Пусть дано некоторое множество чисел, расположенных в определенном порядке:
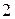 ,
, 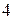 ,
, 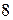 , …,
, …, 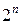 , … (1)
, … (1)
Определение. Числовой последовательностью называется занумерованное множество чисел, расположенных в порядке возрастания их номеров:
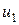 ,
, 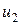 , …,
, …, 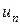 , …,
, …,
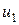 ,
, 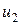 , … – элементы последовательности;
, … – элементы последовательности;
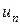 – общий член последовательности: выражение для
– общий член последовательности: выражение для 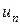 – формула для вычисления любого члена последовательности.
– формула для вычисления любого члена последовательности.
В последовательности (1) 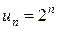 .
.
В математике различают постоянные и переменные величины. Переменные величины, в свою очередь, бывают дискретными и непрерывными.
Пример 1.
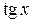 – непрерывная величина; выражение (1) – дискретная величина.
– непрерывная величина; выражение (1) – дискретная величина.
Определение. Переменная величина 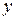 называется ограниченной, если существует число
называется ограниченной, если существует число 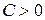 , что для всех своих значений
, что для всех своих значений 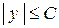 . В противном случае величина
. В противном случае величина 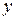 называется неограниченной.
называется неограниченной.
Пример 2.
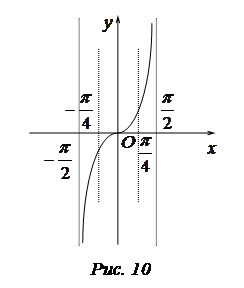 Рассмотрим функцию
Рассмотрим функцию 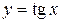
(рис. 10).
Если 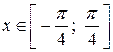 , то функция
, то функция 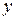 ограниченная, т.к.
ограниченная, т.к. 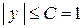 .
.
Если 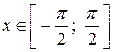 , то функция
, то функция 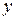 неограниченная.
неограниченная.
Определение. Бесконечно малой (б/м) называется переменная величина 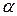 , которая при последовательном изменении по абсолютному значению становится и при дальнейшем изменении остается меньше любой, наперед заданной сколь угодно малой положительной величины
, которая при последовательном изменении по абсолютному значению становится и при дальнейшем изменении остается меньше любой, наперед заданной сколь угодно малой положительной величины 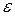 :
: 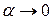 .
.
Пример 3.
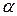 :
: 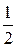 ,
, 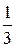 , …,
, …, 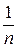 , …
, …
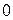 – единственное б/м постоянное число.
– единственное б/м постоянное число.
Определение. Бесконечно большой (б/б) называется переменная величина 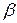 , которая при последовательном изменении по абсолютному значению становится и при дальнейшем изменении остается больше любого, наперед заданного сколь угодно большого положительного числа
, которая при последовательном изменении по абсолютному значению становится и при дальнейшем изменении остается больше любого, наперед заданного сколь угодно большого положительного числа 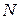 :
: 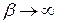 .
.
 2015-02-14
2015-02-14 1710
1710
