Сходимость положительных рядов

1) Критерий сходимости положительного ряда

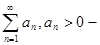положительный ряд (1)

Теорема. Ряд (1) – сходится тогда и только тогда, когда последовательность 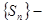ограниченная.

Доказательство. Необходимость.

Известно как необходимое условие сходимости.

Достаточность.

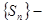ограниченная 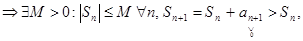т.е. 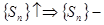сходится (по теореме Коши о пределе монотонной последовательности). Доказано.

Замечание. У положительного ряда достаточно проверять ограниченность только некоторой подпоследовательности частичных сумм.

2) Признак сравнения

Теорема. Если даны два ряда 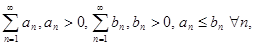то:

1) если 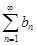- сходится, то 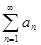- сходится;

2) если 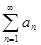- расходится, то 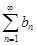- расходится.