Ряды с членами произвольного знака

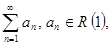
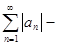ряд с положительными членами (2)

Ряд (1) называется абсолютно сходящимся, если сходится ряд (2).

1) Признак абсолютной сходимости

Абсолютно сходящийся ряд является сходящимся.

Доказательство. Основано на применении критерия Коши.

Ряд (2) – сходится Þ (по критерию Коши) Þ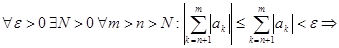

Þ (по критерию Коши) Þ ряд (1) – сходится. Доказано.

Сходящийся ряд (1) называют условно сходящимся, если он абсолютно расходится.

Существуют условно сходящиеся ряды.

Рассмотрим класс знакочередующихся рядов: 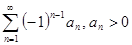(3).

Признак Лейбница.

Если для ряда (3) выполнены условия:

1) 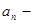невозрастающая;

2)

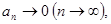
то ряд (3) сходится и справедлива оценка остатка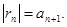

Доказательство. Рассмотрим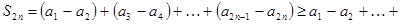

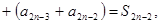т.е. 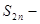неубывающая. С другой стороны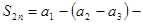

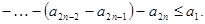Итак, последовательность 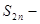неубывающая и ограниченная сверху и 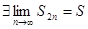. Для последовательности частичных сумм с нечётными номерами 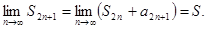Значит,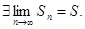

Остаётся оценить остаток: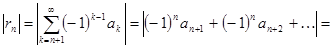

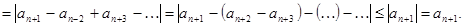
Доказано.

Пример.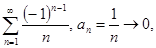

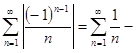расходится

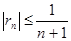
Исходный ряд сходится условно.