Доказательство. 1) подпоследовательность частичных сумм ряда , подпоследовательность частичных сумм ряда

1) 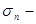подпоследовательность частичных сумм ряда 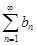, 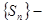подпоследовательность частичных сумм ряда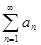 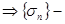ограниченная сверху (по необходимому условию сходимости), 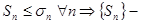ограниченная сверху 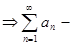сходится.

Вторая часть теоремы доказывается аналогично.

Доказано.

Замечание. В признаке сравнения выполнение неравенства 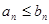достаточно требовать для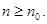

При использовании признака сравнения можно использовать сравнение последовательностей:

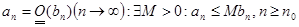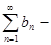1. если и ряд сходится;

2. если 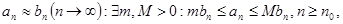то сходимост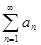и и 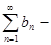эквиваленты;

3. 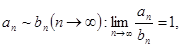то сходимост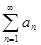и и 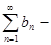эквивалентны.

Пример. Исследовать на сходимость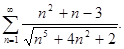

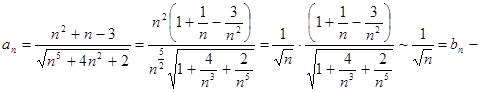расходится, а значит и данный ряд 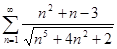расходится.

3) Признак сравнения в предельной форме

Если даны 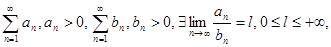то

1) если ряд 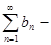сходится, 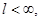то ряд 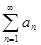- сходится;

2) если ряд 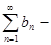расходится, 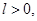то ряд 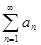- расходится.

4) Обобщённый признак сравнения

Если даны 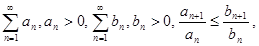то

1) если 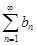- сходится, то 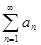- сходится;

2) если 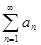- расходится, то 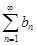- расходится.