- Понятие сходимости числового ряда
Пусть 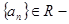 последовательность действительных чисел,
последовательность действительных чисел,
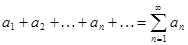 - числовой ряд (1).
- числовой ряд (1).
Составим последовательность частичных сумм:
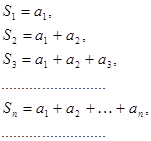
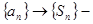 последовательность частичных сумм
последовательность частичных сумм
Если для ряда (1) существует предел последовательность частичных сумм при 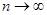 , равный числу
, равный числу 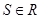 , то ряд называется сходящимся, а число S – его сумма. В противном случае ряд (1) называется расходящимся.
, то ряд называется сходящимся, а число S – его сумма. В противном случае ряд (1) называется расходящимся.
Пример. Исследовать сходимость и найти сумму ряда 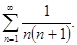
Составляем последовательность частичных сумм:
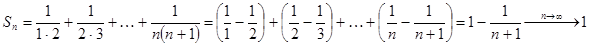
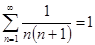
- Свойства сходящихся рядов
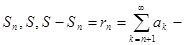 остаток сходящегося ряда,
остаток сходящегося ряда, 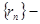 последовательность остатка.
последовательность остатка.
1. Необходимое условие сходимости: частичные суммы сходящегося ряда – ограничены: 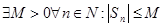 (это вытекает из того, что сходящаяся последовательность ограничена).
(это вытекает из того, что сходящаяся последовательность ограничена).
Приведём пример ряда, у которого частичные суммы ограничены, а сам ряд будет расходиться:
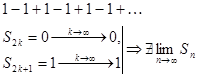
2. Необходимое условие сходимости: у сходящегося ряда предел общего члена равен нулю 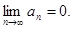
Доказательство. 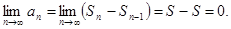 Доказано.
Доказано.
Рассмотрим пример расходящегося ряда, для которого 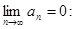
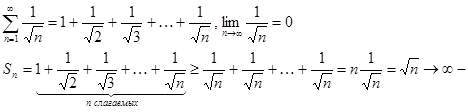
неограниченная, наименьшее слагаемое 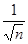 .
.
Пример. 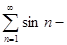 расходится, т.к.
расходится, т.к. 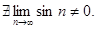
Предположим, что 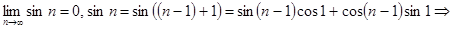
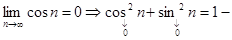 противоречие.
противоречие.
3. Необходимое условие сходимости: у сходящегося ряда 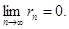
Доказательство. 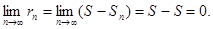 Доказано.
Доказано.
4. Сходимость ряда не нарушится, если добавить или отбросить конечное число слагаемых.
5. Множество сходящихся радов образуют линейное пространство:
если 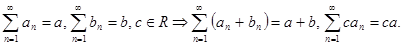
6. Критерий Коши: ряд (1) сходится 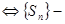 фундаментальная, т.е.
фундаментальная, т.е. 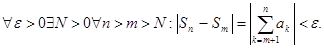
Пример. 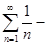 гармонический ряд (расходящийся).
гармонический ряд (расходящийся).
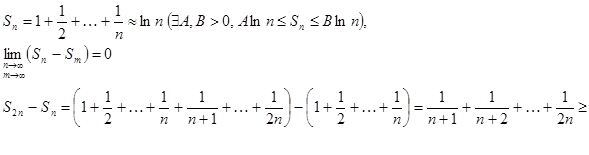
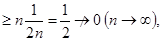 т.е. не выполнен критерий Коши, ряд расходится.
т.е. не выполнен критерий Коши, ряд расходится.
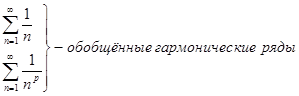
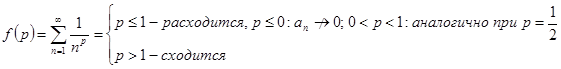
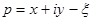 -функция Римана
-функция Римана
Задача. Исследовать сходимость ряда 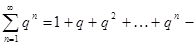 сумма бесконечной геометрической прогрессии. Доказать, что при
сумма бесконечной геометрической прогрессии. Доказать, что при 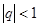 ряд сходится,
ряд сходится, 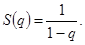
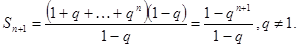
Решение.
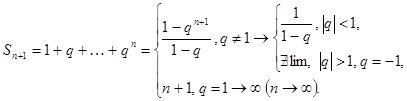
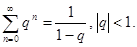
 2015-02-14
2015-02-14 566
566







