Пусть функция 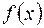 определена на отрезке
определена на отрезке 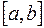 . Разобьем этот промежуток произвольным образом на n частей точками:
. Разобьем этот промежуток произвольным образом на n частей точками:
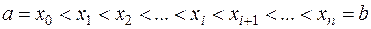 .
.
В каждом из полученных частичных промежутков 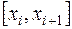 , где
, где 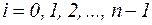 , выберем произвольную точку
, выберем произвольную точку 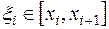 . Вычислим значение функции
. Вычислим значение функции 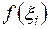 и умножим его на разность
и умножим его на разность 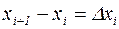 , после этого составим сумму
, после этого составим сумму 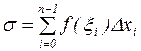 , которая называется интегральной суммой Римана для функции
, которая называется интегральной суммой Римана для функции 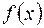 на отрезке
на отрезке 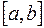 .
.
Пусть 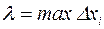 , т.е. длина наибольшего частичного промежутка. Если существует конечный предел интегральной суммы
, т.е. длина наибольшего частичного промежутка. Если существует конечный предел интегральной суммы 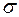 при
при 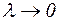 , не зависящий ни от способа разбиения промежутка
, не зависящий ни от способа разбиения промежутка 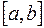 на части, ни от выбора точек
на части, ни от выбора точек 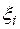 , то этот предел называется определенным интегралом функции
, то этот предел называется определенным интегралом функции 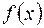 на промежутке
на промежутке 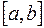 и обозначается символом
и обозначается символом 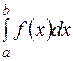 . Таким образом,
. Таким образом, 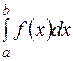
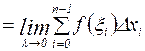 .
.
Функция 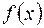 в этом случае называется интегрируемой в промежутке
в этом случае называется интегрируемой в промежутке 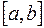 . Числа
. Числа 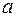 и
и 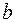 называются соответственно нижним и верхним пределами интеграла.
называются соответственно нижним и верхним пределами интеграла.
Выясним геометрический смысл суммы Римана 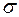 , когда функция
, когда функция 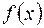 непрерывна и неотрицательна в промежутке
непрерывна и неотрицательна в промежутке 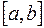 ,
, 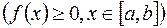 . В этом случае произведение
. В этом случае произведение 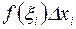 равно площади прямоугольника с основанием
равно площади прямоугольника с основанием 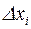 и высотой
и высотой 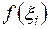 , а сумма
, а сумма 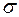 равна сумме площадей прямоугольников с основанием
равна сумме площадей прямоугольников с основанием 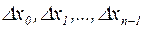 и высотами
и высотами 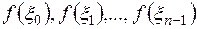 (рис. 1).
(рис. 1).
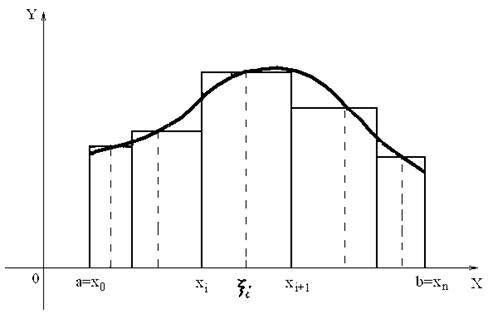
Рис.1
Таким образом, 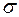 равна площади ступенчатой фигуры, а определенный интеграл равен пределу
равна площади ступенчатой фигуры, а определенный интеграл равен пределу 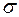 при
при 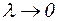 , т.е. площади криволинейной трапеции, ограниченной графиком функции
, т.е. площади криволинейной трапеции, ограниченной графиком функции 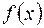 , прямыми
, прямыми 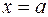 и
и 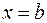 и отрезком
и отрезком 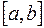 оси
оси 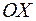 .
.
Свойства определенного интеграла:
Пусть все рассматриваемые функции являются непрерывными, так что определенные интегралы от них существуют. Тогда справедливы следующие соотношения:
1. 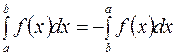

2. 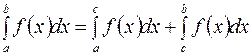
3. 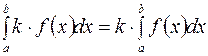
4. 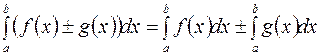
5. 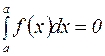
6. Если 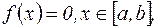 то
то 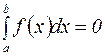 .
.
Если функции 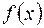 непрерывна на отрезке
непрерывна на отрезке 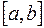 и
и 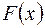 – какая-нибудь первообразная для
– какая-нибудь первообразная для 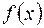 на этом отрезке, то справедлива формула Ньютона-Лейбница:
на этом отрезке, то справедлива формула Ньютона-Лейбница:
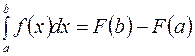 .
.
Правую часть формулы часто обозначают символом 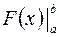 (знак двойной подстановки от
(знак двойной подстановки от 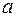 до
до 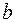 ):
):
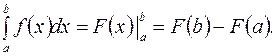
Пример 1. Вычислить определенный интеграл 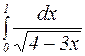 .
.
Решение: 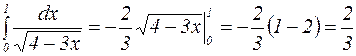 .
.
 2015-02-04
2015-02-04 378
378








