2015-02-04
329
Пусть функция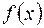 
непрерывна на отрезке 
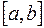, а функция 
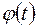определена и непрерывна вместе со своей производной 
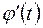на отрезке 
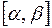, причем 
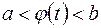для любого 
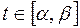и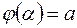 
, 
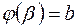
Тогда:
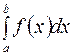
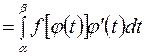
Эта формула называется формулой замены переменной в определенном интеграле.
Пример 2. Вычислить определенный интеграл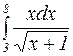 
.
Решение: Сделаем замену переменной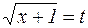 
.
Тогда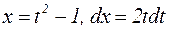 
. Пересчитаем пределы интегрирования: при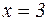 
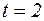, а при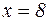 
.
.
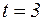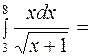
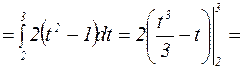
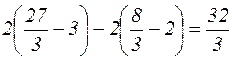Заметим, что при вычислении определенного интеграла к старой переменной не возвращаются.
