Рассмотрим интеграл типа 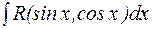 , где R обозначает рациональную функцию своих аргументов
, где R обозначает рациональную функцию своих аргументов 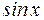 и
и 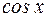 . Интеграл данного типа сводится к интегралу от рациональной функции с помощью так называемой универсальной постановки:
. Интеграл данного типа сводится к интегралу от рациональной функции с помощью так называемой универсальной постановки:
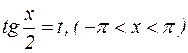 .
.
Действительно, 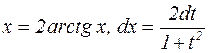 и
и
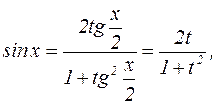
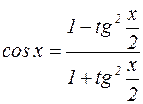 =
= 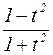 .
.
Тогда, подставляя в данный интеграл вместо 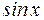 ,
, 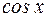 и
и 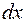 полученные выражения, будем иметь под знаком интеграла рациональную функцию.
полученные выражения, будем иметь под знаком интеграла рациональную функцию.
Пример 13. Вычислить интеграл 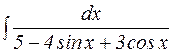 .
.
Решение: Подстановка 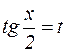 дает:
дает:
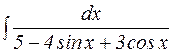 =
= 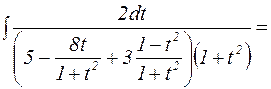
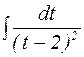 =
= 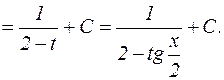
Универсальная подстановка нередко приводит к сложным вычислениям. Поэтому в указанных ниже случаях предпочтительней частные подстановки, также рационализирующие интеграл.
Если 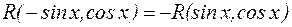 , то применима подстановка
, то применима подстановка 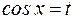 ;
;
если 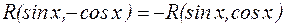 , то применима подстановка
, то применима подстановка 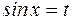 ;
;
если 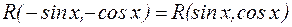 , то применима подстановка
, то применима подстановка 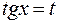 .
.
Пример 14. Вычислить интеграл 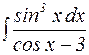 .
.
Решение: Положим 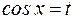 и найдем:
и найдем:
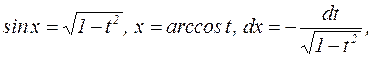 поэтому:
поэтому: 
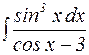 =
= 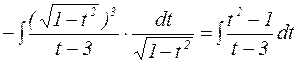 =
= 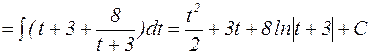 =
= 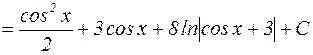 .
.
Рассмотрим интеграл вида 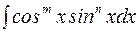 , где m и n – целые числа. Возможны следующие случаи:
, где m и n – целые числа. Возможны следующие случаи:
1. Одно из чисел m или n – нечетное, например 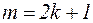 , тогда полагая
, тогда полагая 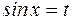 , получим:
, получим:
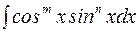 =
= 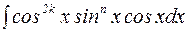 =
= 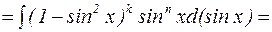
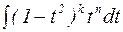 .
.
2. Оба числа m и n – четные. Тогда рекомендуется воспользоваться тригонометрическими формулами понижения степени:
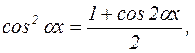
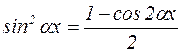 .
.
Пример 15. Вычислить интеграл 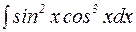 .
.
Решение:
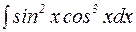 =
= 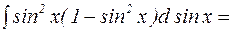
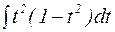 =
= 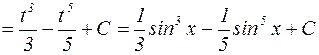 .
.
 2015-02-04
2015-02-04 540
540








