2015-02-14
2942
Несомненно, при изучении методов принятия решений в условиях определенности, возникает вопрос, а как на практике получить оценки привлекательности критериев при качественных альтернативах, как выбрать веса важности критериев. Как ранее было сказано, эти оценки осуществляет либо эксперт (специалист по исследуемому вопросу), либо ЛПР. Практических методов, согласно которым расставляются экспертные оценки, достаточно много. Простейшим (и достаточно популярным) является метод жюри, согласно которому эксперт просто-напросто, в соответствии со своими знаниями, опытом и интуицией, расставляет баллы для каждой альтернативы по имеющемуся критерию по заданной шкале.
Однако на практике не всегда можно точно и пропорционально оценить показатели привлекательности альтернатив, особенно при большом их числе. Гораздо проще бывает попарно сравнить все имеющиеся альтернативы по каждому критерию и оценить, насколько одна конкретная альтернатива привлекательнее другой. Такой метод экспертной оценки получил название метода аналитической иерархии. Рассмотрим его для случая n альтернатив, которые обозначим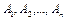 
, и m критериев, обозначенные 
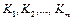. Возьмем первый критерий 
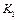и попарно сравним все альтернативы друг с другом по этому критерию. В результате получим матрицу сравнений 
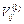, каждый элемент которой, в случае, если альтернатива 
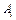не менее предпочтительна чем альтернатива 
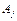равен h. Если же альтернатива 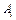не более предпочтительна чем альтернатива 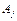, то соответствующий элемент матрицы 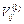равен 1/ h. Так же вычисляются матрицы сравнения 
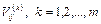для других критериев. Введем, например, такую шкалу сравнений.
|
|
|
Шкала относительной важности парного сравнения альтернатив
| Уровень важности | Степень предпочтительности h |
| Равная важность | |
| Умеренное превосходство | |
| Существенное превосходство | |
| Значительное, большое превосходство | |
| Очень большое превосходство |
При желании можно использовать четные целые числа, выражающие промежуточные уровни предпочтительности. Следует отметить, что эксперт или ЛПР может использовать иные другие шкалы важности парных сравнений.
Аналогично, попарно сравнивая важности критериев, составляется матрица сравнения критериев по которой можно определять их веса.
На следующем этапе вычисляются собственные векторы альтернатив по всех критериям. Для каждой i -й альтернативы по k -му критерию вычисляем элемент вектора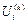 
который равен среднегеометрическому показателей матрицы сравнения для этой альтернативы (строки матрицы):
.
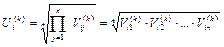Такой же собственный вектор вычисляется и для матрицы сравнения критериев.
|
|
|
Далее в результате нормализации собственных векторов вычисляют веса альтернатив по каждому критерию и веса самих критериев. Вес i -й альтернативы по k -му критерию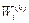 
равен отношению соответствующего элемента собственного вектора к сумме всех элементов собственного вектора данного критерия:
.
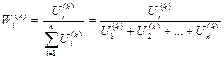Также вычисляются и веса критериев, которые обозначим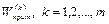 
.
Теперь, имея оценки полезностей альтернатив по всем критериям и веса критериев можно вычислить функции полезности по каждой альтернативе и из их сравнения выбрать наилучшую альтернативу с максимальной функцией. Функция полезности i -й альтернативы вычисляется по формуле:
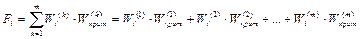
Рассмотрим применение метода аналитической иерархии на примере.
Пример 3. Предприниматель, занимающейся продажей профессионального оборудования для парикмахерских и косметических салонов решил открыть новую торговую точку и построить магазин в одном из районах города. Городские власти предлагают ему под строительство четыре земельных участка: А, В, С и D. В качестве критериев при выборе места строительства предприниматель выделяет три:
- доступность магазина для клиентов (место расположения)– K 1;
- стоимость строительства, доступность коммуникаций – K 2;
- возможность дальнейшего расширения (планируется со временем пристроить помещения для дополнительных отделов) – K 3.
Предприниматель, выступая экспертом по первому критерию о доступности и месторасположения магазина сравнил альтернативы и решил, что А по сравнению с В имеет умеренное преимущество (балл 3), А по сравнению с С имеет значительное превосходство (балл 7) и А по сравнению с D – существенное превосходство (балл 5). Эти баллы записываем в первую строку таблицы. Сравнивая альтернативы В и С, эксперт решил, что В имеет превосходство большее, чем умеренное и менее, чем существенное, поэтому в таблицу на соответствующую позицию было решено занести балл 4. Альтернатива В по сравнению с D имеет умеренное превосходство, а С и D имеют равную важность. В результате таблица примет вид:
Критерий «Доступность магазина для клиентов»
| Альтернативы | A | B | C | D |
| A | ||||
| B | 1/3 | |||
| C | 1/7 | 1/4 | ||
| D | 1/5 | 1/3 |
По аналогии, эксперты по двум другим критериям сравнили попарно все альтернативы и получили следующие результаты.
Критерий «Стоимость строительства»
| Альтернативы | A | B | C | D |
| A | 1/7 | 1/3 | ||
| B | 1/5 | 1/3 | 1/7 | |
| C | ||||
| D | 1/3 |
Критерий «Возможность расширения»
| Альтернативы | A | B | C | D |
| A | 1/3 | 1/7 | ||
| B | 1/3 | 1/3 | 1/5 | |
| C | 1/2 | |||
| D |
Следующий этап состоит в сравнении важностей самих критериев. Предприниматель считает самым важным первый критерий, он имеет умеренное превосходства над вторым и существенное над третьим. Второй критерий имеет умеренное превосходство над третьим. В результате получаем матрицу:
| Критерий | K 1 | K 2 | K 3 |
| K 1 | |||
| K 2 | 1/3 | ||
| K 3 | 1/5 | 1/3 |
Третий этап состоит в расчете собственных векторов и весов альтернатив по каждому критерию. Для первого критерия «Доступность магазина для клиентов» собственный вектор альтернативы А равен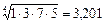 
, Для второй, третьей и четвертой альтернативы собственные вектора равны: 
, 
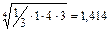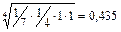и 
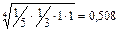соответственно.
Рассчитаем теперь веса альтернатив. Просуммируем элементы собственного вектора: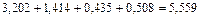 
. Разделим каждый элемент собственного вектора на эту сумму, получим нормализованные веса каждой альтернативы, а именно, для альтернативы А: 3,202/5,559=0,576, для других альтернатив, аналогично, 0,254, 0,078, 0,092. Следует отметить, что в сумме веса должны давать единицу. Запишем результат в таблицу:
Критерий «Доступность магазина для клиентов»
| Альтернативы | A | B | C | D | Собственный вектор | Вес |
| A | 3,201 | 0,576 | ||||
| B | 1/3 | 1,414 | 0,254 | |||
| C | 1/7 | ¼ | 0,435 | 0,078 | ||
| D | 1/5 | 1/3 | 0,508 | 0,092 |
сумма 5,559
|
|
|
Аналогичные таблицы составляем и для случая парного сравнения альтернатив по другим критериям.
Критерий «Стоимость строительства»
| Альтернативы | A | B | C | D | Собственный вектор | Вес |
| A | 1/7 | 1/3 | 0,699 | 0,128 | ||
| B | 1/5 | 1/3 | 1/7 | 0,312 | 0,057 | |
| C | 2,817 | 0,517 | ||||
| D | 1/3 | 1,627 | 0,298 |
сумма 5,452
Критерий «Возможность расширения»
| Альтернативы | A | B | C | D | Собственный вектор | Вес |
| A | 1/3 | 1/7 | 0,615 | 0,111 | ||
| B | 1/3 | 1/3 | 1/5 | 0,386 | 0,070 | |
| C | 1/2 | 1,656 | 0,298 | |||
| D | 2,893 | 0,521 |
сумма 5,550
Таким же способом вычисляем собственные вектора и веса критериев. Единственное отличие при вычисление собственных векторов состоит в том, что число критериев равно трем (а число альтернатив – четыре), поэтому из произведения парных оценок сравнений нужно брать корень третьей степени. Например для критерия K 1: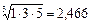 
. Результаты – в таблице:
| Критерий | K 1 | K 2 | K 3 | Собственный вектор | Вес |
| K 1 | 2,466 | 0,637 | |||
| K 2 | 1/3 | 0,258 | |||
| K 3 | 1/5 | 1/3 | 0,405 | 0,105 |
сумма 3,871
Рассчитываем функции полезности для каждой альтернативы:
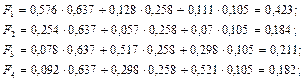
Видно, что максимальная функция полезности соответствует первой альтернативе А, следовательно, данный участок и следует выбрать для строительства.
Способы решения задач принятия решений методом аналитической иерархии с использованием ЭВМ приведены в лабораторной работе № 2 данного пособия.
