Семейства случайных величин

ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ

В практике научных исследований и технических разработок случайные процессы в настоящее время занимают столь большое место, что без создания эффективных методов их описания и изучения нельзя говорить о дальнейшем научно-техническом прогрессе.

Дать формальное определение случайного процесса, сочетающее в себе физическую сущность и математическую строгость, чрезвычайно трудно. Интуитивные представления о случайном процессе связаны в основном с непредсказуемостью его мгновенных значений. Математически строгое определение требует введения понятия ансамбля, т.е. бесконечной совокупности реализаций. С физической точки зрения вполне допустимо представление случайного процесса одной реализацией. С математической точки зрения отдельная реализация является детерминированной функцией времени, с помощью которой определить статистические свойства процесса можно лишь при выполнении определенных условий.

Выбор целесообразного уровня строгости описания случайных процессов при решении прикладных задач в значительной степени определяет качество получаемых результатов [1]. Вместе с тем уровень строгости описания должен соответствовать уровню представлений и характеру решаемых задач.

Семейства случайных величин

С точки зрения практических приложений [2] любая меняющаяся система, находящаяся под влиянием случайных факторов, представляет собой случайный процесс. В соответствии со сказанным случайный процесс может быть охарактеризован как процесс, мгновенное значение которого в произвольный момент времени представляет собой случайную величину [1].

Рассмотрим простой случай, когда состояние системы достаточно хорошо определяется одной количественной характеристикой. Эта величина x(t) в каждый фиксированный момент t не является однозначно определенной, как в случае детерминированных систем, а зависит от случайных факторов, которые влияли на систему до момента t. При построении математической модели этого процесса естественно рассматривать x(t) в каждый фиксированный момент t как случайную величину, определенную на некотором вероятностном пространстве (W, F, P). Когда t меняется в рассматриваемом промежутке времени, получаем семейство случайных величин x(t), зависящих от параметра t и определенных на одном и том же вероятностном пространстве. Элементарными событиями w в этом вероятностном пространстве будут возможные исходы случайного эксперимента, который определяет поведение системы в целом.

Пусть (W, F, Р) – некоторое вероятностное пространство, T – множество значений параметра. Случайным процессом называется конечная вещественная функция x(t, w),которая при каждом фиксированном t Î T является измеримой функцией от w Î W.

Легко получить обобщенную форму этого определения в случае, когда для полного описания состояния системы при каждом фиксированном значении параметра t необходимо знать несколько величин x₁(t),..., x _n (t). Если рассматривать x _j (t) как компоненты случайного вектора x (t, w) = = {x₁(t, w),..., x _n (t, w)}, то семейство случайных векторов, получающееся при изменении t на множестве Т, будет определять векторный случайный процесс.

Итак, x(t) – случайный процесс. При каждом фиксированном t = t ₁ случайная величина x(t ₁) = (t ₁, w) имеет определенное распределение вероятностей, функцию распределения которой обозначим F (x, t ₁) = P {x(t ₁) £ £ x }.

Пусть t ₁,..., t_n – произвольное конечное множество значений t. Соответствующие случайные величины x(t ₁),..., x(t_n) имеют совместную функцию распределения

F (х ₁,..., х_n, t ₁,..., t_n) = Р {x(t ₁) £ х ₁,..., x(t_n) £ x_n }.

Семейство таких совместных распределений для n = 1, 2,... и всех возможных значений t_j называется семейством конечномерных распределений процесса x(t). Это одно из основных понятий теории, и многие существенные свойства случайного процесса определяются свойствами семейства его конечномерных распределений. Конечномерные распределения случайного процесса должны удовлетворять условиям симметрии и согласованности.

Условие симметрии требует, чтобы n -мерные функции распределения, введенные выше, были симметричными по всем параметрам (х_j, t_j), т.е. чтобы эти функции распределения не менялись при одновременной перестановке х_j и t_j.

Условие согласованности выражается соотношением

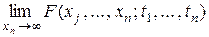= F (x_j,..., x_{n -1}; t ₁,..., t_{n -1}),

которое следует из очевидного факта: w – множество, определенное неравенствами

x(t ₁) £ x ₁,..., x(t_{n -1}) £ x_{n -1}, x(t_n) £ x_n,

при x_n ® ¥ приближается к множеству

{w, x(t1) £ x1,..., x(tn-1) £ xn-1}.

Два случайных процесса x(t) и h(t) называются эквивалентными, если при каждом фиксированном t множества значений параметра x(t) и h(t) являются эквивалентными случайными величинами, так что x(t) = h(t) с вероятностью единица. Очевидно, семейства конечномерных распределений у эквивалентных процессов совпадают.