Простейший входящий поток

Определение. Простейшим потоком называется стационарный ординарный поток без последействия. Простейший поток вызовов является наиболее распространенной моделью реального потока заявок, применяемой в системах массового обслуживания. В большинстве задач прикладного характера замена реальных потоков на простейшие с теми же интенсивностями приводит к получению решения, которое мало отличается от истинного [7]. Математическое моделирование показало [7], что в большинстве случаев эта погрешность ограничена 3–5 % и лишь в редких случаях 10–12 %, что вполне приемлемо при решении прикладных задач. Однако, как указано в работах [8–10], имеются особые условия, когда эта погрешность может достигнуть значительных величин. В связи с этим необходимо использовать модели потоков более сложного характера.

Математическая модель простейшего потока. Определим вероятности поступления потока k (k = 1, 2, …) вызовов на отрезке времени [ t ₀, t ₀+ t): P_k (t ₀, t ₀+ t). Исследования будем проводить на отрезке времени [ t ₀, t ₀+ t + t), который можно представить состоящим из двух примыкающих друг к другу отрезков [ t ₀, t ₀+ t + t) = [ t ₀, t ₀+ t) + [ t, t + t).

Для того чтобы в течение отрезка [ t ₀, t ₀+ t + t) поступило точно k вызовов, необходимо, чтобы за первый промежуток времени [ t ₀, t ₀+ t) поступило k, или k –1, …, или k – i, …, или 0 вызовов, а за второй промежуток соответственно 0, или 1, …, или i, …, k вызовов.

Введем обозначения: P_k [ t ₀, t ₀+ t + t) – вероятность поступления точно k вызовов за отрезок времени [ t ₀, t ₀+ t + t); P_k-i [ t ₀, t ₀+ t) – вероятность поступления k - i вызовов за первый отрезок времени [ t ₀, t ₀+ t); P_i [ t, t + t) – вероятность поступления точно i вызовов за второй отрезок времени [ t, t + + t). Согласно определению простейший поток является стационарным. Из этого следует, что вероятности поступления того или иного числа вызовов (заявок) за отрезки времени [ t ₀, t ₀+ t + t); [ t ₀, t ₀+ t), [ t, t + t) не зависят от моментов начала отсчета времени, а зависят только от длины отрезков времени. Поэтому упростим обозначения как отрезков, так и вероятностей: [ t ₀, t ₀+ t + t) будем обозначать как [ t + t); [ t ₀, t ₀+ t) – как [ t); [ t, t + t) – как [t); P_k (t ₀, t ₀+ t + t) – как P_k (t + t); P_k-i (t ₀, t ₀+ t) – как P_k-i (t); P_i (t, t + t) – как P_i (t).

Простейший поток – это поток без последействия. Поэтому независимыми являются события, заключающиеся в поступлении какого-либо числа вызовов за первый и второй промежутки времени, и вероятность поступления точно k вызовов за время [ t + t) для каждой регистрации i = 0, 1, …, k составляет P_k (t + t) _i = P_k-i (t) P_i (t), i = 0, 1, …, k. Поскольку реализации с i = 0, 1, …, k представляют несовместимые события, то согласно формуле полной вероятности имеем

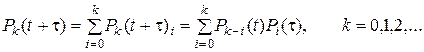(2.3)

Выражение (2.3) представляет собой систему, состоящую из бесконечного числа уравнений. Устремим отрезок времени t к нулю. Вследствие ординарности простейшего потока p₂(t, t – t) = 0(t), t ® 0. Вероятности поступления 2, 3, … вызовов: P ₂(t), P ₃(t) и т.д. – есть бесконечно малые более высокого порядка по отношению к t. Следовательно, в системе уравнений (2.3) вероятности P_i имеют конечные значения только при i, равном 0 и 1. На основании этого (2.3) преобразуется к виду