Постановка задачи. Ранее рассмотрена СМО с конечной очередью и неоднородными запросами на число мест в очереди. При этом, как отмечено, главная сложность применения ВМО – высокая размерность модели, что для реальных значений параметров технических систем исключает возможность ее применения. Поэтому весьма актуальной является задача построения СМО, которая позволяла бы вести расчет вероятностных характеристик, ориентируясь на потребности проектировщиков. Для решения этой задачи введем ряд упрощений: во-первых, запросы на число мест в очереди однородны (это означает, что любая заявка требует, при занятости обслуживающих приборов, фиксированное (постоянное) число мест в очереди); во-вторых, длина очереди бесконечна (т.е. имеется буфер бесконечной длины).
Оригинальная СМО с учетом приведенных ограничений – это N- линейная СМО с буфером, на вход которой поступает простейший с параметром l поток заявок. Каждая заявка для своего обслуживания с вероятностью q (m) требует m приборов. Если буфер свободен, а в системе имеется достаточное число свободных приборов, то заявка немедленно начинает свое обслуживание, занимая требуемое число m приборов. Если в системе недостаточно свободных приборов для обслуживания поступившей заявки, то она становится в очередь для ожидания. Если в буфере имеются заявки, то поступившая заявка также становится в очередь.
Времена обслуживания приборами независимы и одинаково распределены как для одной, так и для разных заявок. Будем считать, что время обслуживания экспоненциальное с параметром m.
Для исследования указанной СМО рассмотрим случайный процесс 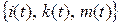 . Здесь i (t) – число заявок в очереди, k (t) – число свободных приборов, m (t) – число приборов, требуемых заявкой, которая в момент t стоит первой в очереди. Если i (t) = 0, то компонент m (t) не формируется, а функционирование СМО определяется единственным компонентом h (t) – числом занятых приборов.
. Здесь i (t) – число заявок в очереди, k (t) – число свободных приборов, m (t) – число приборов, требуемых заявкой, которая в момент t стоит первой в очереди. Если i (t) = 0, то компонент m (t) не формируется, а функционирование СМО определяется единственным компонентом h (t) – числом занятых приборов.
В силу того, что информация о числе приборов, требуемых для обслуживания заявки, стоящей в очереди, не используется до того момента, пока эта заявка не станет первой в очереди, а числа требуемых приборов для различных заявок независимы, рассматриваемый случайный процесс является марковским. Для его стационарных вероятностей
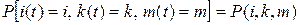 (4.6)
(4.6)
можно построить следующую систему уравнений:
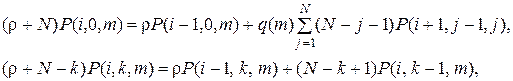 (4.7)
(4.7)
здесь 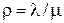 , 0 < m < N + 1, 0 < k < m.
, 0 < m < N + 1, 0 < k < m.
Для существования стационарных вероятностей (4.6) необходимо ограничить загрузку r некоторой величиной S, значение которой определим ниже.
Для решения (4.7) воспользуемся методом [11], для этого введем положительный малый параметр e > 0, значение которого также определим ниже, и в (4.7) сделаем замену:
i e = x, 1/e P (i, k, m) = P(x, k, m). (4.8)
Тогда для системы (4.8) получим
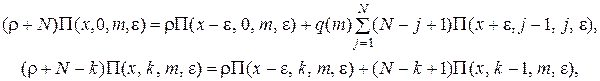
0 < k < m.
Раскладывая функции П(х ± e, k, m, e) в ряд по степеням e в окрестности точки (x, k, m, e) и ограничиваясь слагаемыми порядка e2, получим систему:
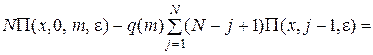
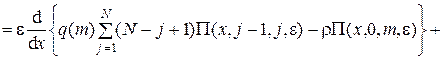
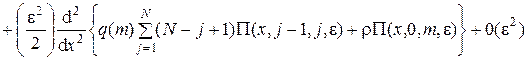 , (4.9)
, (4.9)
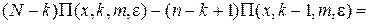
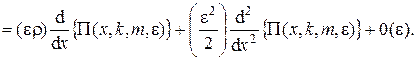
Систему (4.9) будем решать в три этапа при e ® 0. Метод асимптотического анализа [11] полагает, что при e ® 0 величина загрузки r сходится к своему предельному значению S. Здесь S – точная верхняя граница тех значений загрузки r, при которых рассматриваемая система имеет стационарный режим.
Этап 1. В системе (4.9) положим e = 0 и, обозначив P(x, km, 0) = P(x, k, m), получим однородную систему алгебраических уравнений:
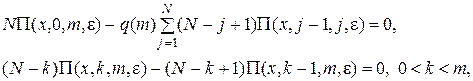
решение которой определяется с точностью до величины f (x), постоянной по k и m, в виде 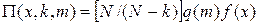 .
.
Этап 2. Найдем решение системы (4.9) с помощью e в виде
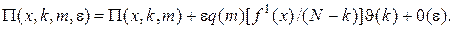 (4.10)
(4.10)
Подставив (4.10) в (4.9) и положив r = S, получим для J(k) неоднородную систему линейных алгебраических уравнений:

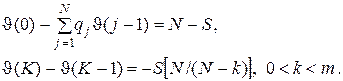 (4.11)
(4.11)
Из второго уравнения (4.11) для k ³ 1 можно записать
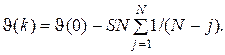 (4.12)
(4.12)
Чтобы (4.12) было решением системы (4.11), необходимо выполнение равенства
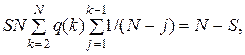
которое получается при подстановке (4.12) в первое уравнение системы (4.11) и определяет значение величины
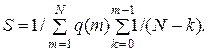 (4.13)
(4.13)
Величина S, являясь пропускной способностью СМО, определяет одну из самых основных характеристик системы, ограничивая предельную загрузку, позволяя функционировать ей в стационарном режиме.
Этап 3. Для нахождения величины f (x) просуммируем по k и m все уравнения (4.9) и получим равенство
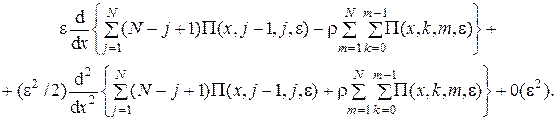
 2015-02-14
2015-02-14 438
438








